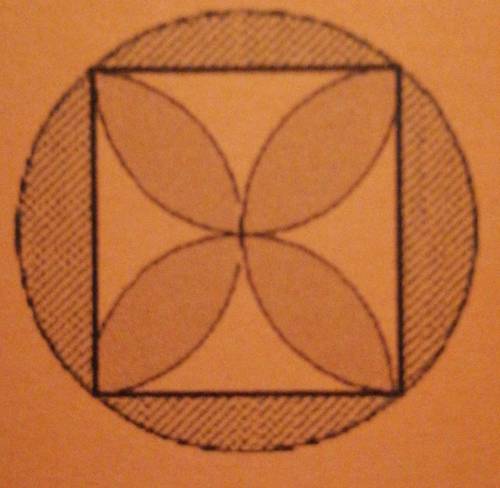
Квадрат вписано в круг. Всередині квадрата побудовано півкруги на його
сторонах як на діаметрах. Чотири
попарних перетини цих кругів утворюють
фігуру «квітка». Доведіть, що площа цієї
«квітки» дорівнює площі частини
описаного круга, що лежить поза
Квадратом.​

elenakovaleskau    2   04.11.2020 22:20    3