Куб, все грани которого окрашены, распилен на 64 кубика одинакового размера. какова вероятность того, что среди случайно отобранных двух кубиков оба имеют по дае окрашенные стороны.

Ответы

BOSS653 08.10.2020 21:12

Куб распилили на 64 одинаковых кубика. Так как объем куба считается по формуле V = a³ = 64, значит, каждое ребро распилили на 4 части:

V = 4³ = 64

Тогда окрашенными с двух сторон окажутся по 2 не угловых кубика вдоль каждого ребра (на рисунке - зеленого цвета).

У куба 12 ребер : 4 верхних, 4 нижних и 4 боковых.

Тогда окрашенными с двух сторон окажутся 2*12 = 24 кубика.

Итак, нужных кубиков - 24.

Всего - 64

Вероятность, что первый вытянутый с двумя окрашенными гранями :

p₁ = 24/64 = 3/8

Вероятность, что второй вытянутый с двумя окрашенными гранями :

p₂ = 23/63

Вероятность, что оба кубика нужные

p = p₁*p₂ =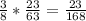 $\frac{3}{8} *\frac{23}{63} =\frac{23}{168}$

по формулам

Благоприятные события - сочетание 2 кубиков из 24 без повторений

$C_{24}^2=\frac{24!}{(24-2)!*2!} =\frac{22!*23*24}{22!*2} =23*12=276$

Все события - сочетание 2 кубиков из 64 без повторений

$C_{64}^2=\frac{64!}{(64-2)!*2!} =\frac{62!*63*64}{62!*2} =63*32=2016$

Вероятность

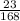$p=\frac{276}{2016} =\frac{23}{168}$

ответ: р= $\frac{23}{168}$ ≈ 0,137

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Математика

moyutot 10.12.2019 13:05

timofeyzel 10.12.2019 13:06

Вар 1,11,21 #1 и есть час на решение...

Zeinalovag 10.12.2019 13:07

kiryazhigulski 10.12.2019 13:09

Vergoon 10.12.2019 13:10

ХацуноМико 10.12.2019 13:10

1246881 10.12.2019 13:10

maschavyaznina 10.12.2019 13:11

ElenaScience 10.12.2019 13:11

Решить действия расписать (58+x)-23=96...

DiroL21 10.12.2019 13:11