"Комплексные числа" 1. Найти значение корня: 
2. Записать в алгебраической форме: 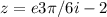
Другие вопросы по теме Математика
Популярные вопросы
- Завтра нужно сочинение по любимой главе отрочества л.н.толстого...
3 - Срешением все расписать надо материальная точка движется прямолинейно...
3 - Написать пять предложений с причастиями из новеллы старик в станционном...
1 - Іте напісать сачыненне на тэму мой любімы герой у аповесці васіля быкава...
3 - 1.типы желёз 2.куда выделяются секреты 3.примеры желёз...
2 - Напишите 5 предложений с неопределенными местоимениями! )...
1 - Составт и запишите предложения с данными причастными оборотами, употребления...
2 - Составьте предложения со словами непреклонно,задумчиво,терпеливо только...
1 - Ккаким двум типам можно свести все разнообразие растительных клеток?...
2 - Сформулируйте и докажите теорему об отношении площадей подобных треугольников,...
2
Для этого мы можем представить данное число в алгебраической форме и затем использовать формулу для нахождения корня! Таким образом, пусть
Теперь запишем это комплексное число в алгебраической форме:
В нашем случае a =
Теперь применим формулу для нахождения корня комплексного числа:
Подставляя значения a и b:
w =
Таким образом, значение корня комплексного числа
2. Запишем число
Для этого нам необходимо использовать формулу Эйлера, где e - экспонента, и заданное число записывается как z = e^(θi), где θ - угол в радианах.
Итак, в нашем случае, z = e^(3π/6i-2).
Для начала, запишем e^(3π/6i) в тригонометрической форме:
e^(3π/6i) = cos(3π/6) + isin(3π/6).
Рассчитаем это:
cos(3π/6) = cos(π/2) = 0
sin(3π/6) = sin(π/2) = 1.
Тогда e^(3π/6i) = 0 + i = i.
Теперь представим число -2 в алгебраической форме: -2 - 0i.
Итак, z = e^(3π/6i-2) = i - 2.
Таким образом, число