Найти частное решение дифференциального уравнения, удовлетворяющее начальную условие в (Хо) = Уо Знайти частинний розв'язок диференціального рівняння,що задовольняє початкову умову у(Хо)=Уо

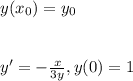
$y(x_{0} )=y_{0} \\\\\\y'=-\frac{x}{3y} ,y(0)=1$

Ответы

Sevinch94 05.01.2021 16:24

Пошаговое объяснение:

$y' = - \frac{x}{3y} \\ \frac{dy}{dx} = - \frac{x}{3y} \\ \int\limits \: ydy = - \frac{1}{3} \int\limits \: xdx \\ \frac{ {y}^{2} }{2} = - \frac{1}{3} \times \frac{ {x}^{2} }{2} + C \\ {y}^{2} = - \frac{1}{3} {x}^{2} + C$

общее решение

y(0) = 1

$1 = 0 + C \\ C = 1$

Частное решение:

${y}^{2} = - \frac{ {x}^{2} }{3} + 1$

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Математика

akkusha1 24.04.2020 13:09

Подробно объясните как получилась 3 строчка в уравнении...

rubyrose2003 24.04.2020 13:08

Круг разделили на 4 равные части, затем какдую часть разделили ещё на 3 равные части. НаСКОЛЬКО частей разделился круг? Сколько такихчастей составит: целый круг1/2 круга;...

прииииииип 24.04.2020 13:09

1)5t-6t 2)4a+7a-2a Тема: Возведение подобных слагаемых...

javajaaripo 24.04.2020 13:09

1. Раскройте скобки и найдите значение выражения: 4,49 - (6,21 + 3, 3) + (6,7 - 4,49) + 6,21. 2. Решите уравнение: -7(3x - 8) + 3(4x + 5) = 8. 3. Приведите подобные слагаемые:...

LIZA555666777 24.04.2020 13:08

Правда что тут обманывают А ну да я и сам знаю ответ ДА!...

KarinaKotik11 24.04.2020 13:08

(2x-5)(3x+7)=0 решите уравнение...

SeyshellaGoa 24.04.2020 13:08

БЫСТРЕЙ МАТЕМАТИКА.Радиус окружности равен 17,97 см. Значение числа π≈3,14.Определи длину C этой окружности (с точностью до сотых).Длина окружности равна 11,147 см. Значение...

даша3549 24.04.2020 13:08

Периметр параллелограмма составляет 126 м. Известно, что один край в 6 раз длиннее другого.Рассчитайте длину ребер параллелограмма!Самый короткий край мСамый длинный край...

X1ТихийСнайпер1X 24.04.2020 13:08

умоляю! На меня мама кричит ...

какчитаетсяэтосказка 24.04.2020 13:08

Площадь участка 234м(в квадрате).Длина участка 26м.Чему равна ширина этого участка? За правельно решонную задачу...

Популярные вопросы