Комбинаторика.
С3 8-А2 6
Подробно!
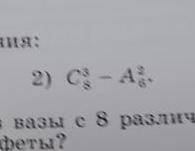
Другие вопросы по теме Математика
Популярные вопросы
- По таблица европа в 18 веке .должно получиться 8 стран. 20 !...
3 - За 1ача 14чтобы принести царю-батюнести царю-батюшке молодильные яблоки,...
1 - Угадайте корень уравнения: 1) 7х = 7,49 , 2) 9,6 : х = 8 , 3) х * 12...
1 - Составить условие и решение .для посадки 100 саженцев.перед школой посадили...
1 - Длина прямоугольника 5см,аширина на 2см больше.стороны увеличили на 8см.чему...
2 - No 2интернет-провайдер хочет проложить новуюсеть. в стране 7 городов,...
1 - Ть як удосконалити текст хліб- найбільше багатство текст скину в друзья...
1 - Тапсырмасұрақтарға жауап беріңіз, өлеңдегі негізгі ақпараттарды анықтаңыз.1....
1 - 6. вкажіть протонні числа елементів, що належать до однієї групи.а) 20;...
3 - Кие укрепление организмы предлагаются что их предложеного вы считаете...
2
В комбинаторике С(n, k) обозначает количество сочетаний из n по k, а А(n, k) обозначает количество размещений из n по k.
Сочетаниями называются наборы объектов (элементов), в которых порядок не имеет значения. При этом один и тот же объект может входить в сочетание только один раз.
Размещениями называются наборы объектов (элементов), в которых порядок имеет значение. При этом один и тот же объект может входить в размещение несколько раз.
Теперь приступим к решению конкретной задачи.
Дано выражение "С3 8-А2 6". Нам нужно вычислить значение этого выражения. Для начала разберемся с С3 8, что означает сочетания из 8 по 3.
Количество сочетаний из 8 по 3 можно вычислить по формуле:
C(n, k) = n! / (k! * (n - k)!)
где n! - факториал числа n.
Таким образом, для нашего случая, мы должны вычислить:
C(8, 3) = 8! / (3! * (8 - 3)!)
Выполним вычисления:
8! = 8 * 7 * 6 * 5 * 4 * 3 * 2 * 1 = 40 320
3! = 3 * 2 * 1 = 6
5! = 5 * 4 * 3 * 2 * 1 = 120
Подставим значения в формулу:
C(8, 3) = 40 320 / (6 * 120)
C(8, 3) = 40 320 / 720
C(8, 3) = 56
Таким образом, сочетаний из 8 по 3 равно 56.
Теперь перейдем ко второй части выражения "А2 6", где нужно посчитать размещения 2-х элементов из 6-ти.
Количество размещений из 6 по 2 можно вычислить по формуле:
А(n, k) = n! / (n - k)!
где n! - факториал числа n.
Применяя эту формулу к нашему случаю, мы должны вычислить:
A(6, 2) = 6! / (6 - 2)!
Выполним вычисления:
6! = 6 * 5 * 4 * 3 * 2 * 1 = 720
4! = 4 * 3 * 2 * 1 = 24
Подставим значения в формулу:
A(6, 2) = 720 / 24
A(6, 2) = 30
Таким образом, размещений 2-х элементов из 6-ти равно 30.
Теперь мы можем объединить полученные значения и подставить их в исходное выражение "С3 8-А2 6":
С3 8-А2 6 = 56 - 30
С3 8-А2 6 = 26
Таким образом, значение выражения "С3 8-А2 6" равно 26.