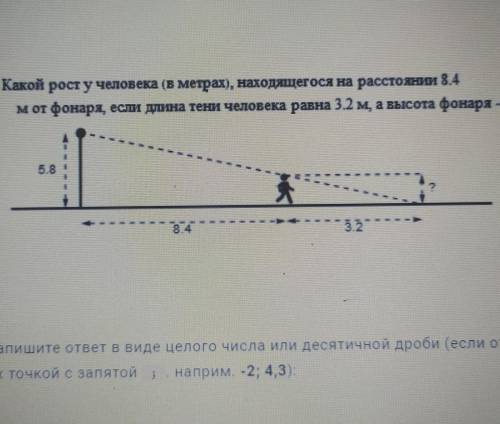
Какой рост у человека (в метрах), находящегося на расстоянии 8,4м от фонаря, если длина тени человека равна 3,2м, а высота фонаря 5,8м?
Другие вопросы по теме Математика
Популярные вопросы
- Скажите как решать примеры такова типа : 807x600 , 803x400 и т.д....
2 - Для калия красная граница фотоэффекта 564 нм. определите значение запирающего...
3 - Какие элементы народных сказок вы видите в этом отрывке? из руслан и...
1 - Варах: 27га,8 га 3а,96 000 м2,9км2,34а...
2 - Выражение. оно легкое, но я уже забыла все. , . (а+3) в квадрате - 2а(3-4а)...
1 - Решить и записать решение 2 класс : синеглазка начертила 5 разноцветных...
1 - Написать сочинение на тему волшебный горшок который умел сам варить кашу...
1 - Львёнок утёнок ёжик слонёнок в каком слове звуков больше чем букв...
3 - Бразилия занимает первое место в мире по производству: а)кофе б)кофе...
2 - Что надо изменить в спектральном аппарате, если вместо призмы использовать...
3
Чтобы решить эту задачу, нам понадобятся пропорции. Давайте обозначим рост человека, который нужно найти, как х.
Мы знаем, что фонарь создает тень длиной 3,2 метра на поверхности земли и находится на расстоянии 8,4 метра от человека.
Теперь мы можем записать пропорцию:
$$ \frac{5,8}{x} = \frac{8,4}{3,2} $$
Для решения этой пропорции нам необходимо найти значение x. Для этого нам нужно перемножить числа на противоположных концах пропорции и приравнять их.
$$ 5,8 \cdot 3,2 = 8,4 \cdot x $$
$$ 18,56 = 8,4x $$
Теперь делим обе стороны уравнения на 8,4, чтобы изолировать x:
$$ x = \frac{18,56}{8,4} $$
$$ x ≈ 2,205 $$
Таким образом, рост человека, находящегося на расстоянии 8,4 метра от фонаря, составляет около 2,205 метра.
Надеюсь, эта информация будет полезной! Если у вас возникнут еще вопросы, не стесняйтесь обратиться!