1. Математика
  2. Как вычислять синусы и косинусы?

Как вычислять синусы и косинусы?

sedvl sedvl    3   02.12.2020 15:27    0

Ответы
RihDest RihDest  02.12.2020 15:30

ДА

Пошаговое объяснение:

Приближенное число для каждой из известных функций можно найти по определению. Для одних можно указать точные значения, для других – только приблизительные.

Линии тригонометрических функций – это линии, которые изображаются вместе с единичной окружностью. Они имеют точку отсчета и единичный отрезок, которая равна единице в координатной системе. Они используются для наглядного изображения значений.

Для того, чтобы найти синус по известному косинусу,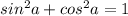  sin^{2} a+cos^{2} a=1

Тангенс по известному косинусу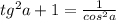 tg^{2} a+1=\frac{1}{cos^{2}a }

Котангенс по известному синусу или наоборот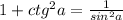 1+ctg^{2} a=\frac{1}{sin^{2}a }

Тангенс через котангенс или наоборот можно найти благодаря удобной формуле: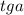 tga × ctg a=1

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
EnemySSS EnemySSS  05.04.2021 18:17
8. Сторона ромба равна 1, острый угол равен 30°. Найдите радиус вписанной окружности этого ромба....
Черепашка312 Черепашка312  05.04.2021 18:17
запишите ответ периодическими дробями 1) 14 :3 = 2) 11:6 = 3) - 9,9 : 33 = 4) 10,25 : 11 = 5) 30,2 : 15 = 6) 22 : (-9) = 7) -4:(-240) = 8) -911 : 18 =...
Супер1009 Супер1009  05.04.2021 18:17
Рост младшего брата равен 0,97 м. Каков приблизительный рост старшего брата? ответ запиши в сантиметрах....
Djjdcnudghu Djjdcnudghu  05.04.2021 18:16
Выразите в метрах4 целых 3/5км​...
котик8308 котик8308  05.04.2021 18:16
Придумай и реши задачи по вырожениям а) (180+120) :60:​...
Masha6655 Masha6655  05.04.2021 18:16
Сумма трёх чисел равна 255. Первое число составляет 12 % этой суммы. Второе число в 3 раза больше первого. Найди третье число....
bodisss bodisss  05.04.2021 18:15
решить тригонометрические неравенства, от...
Христя2017 Христя2017  05.04.2021 18:14
451. Площадь одного поля равна 103,6 га, площадь второго - на 32 га больше С каждого гектара первого поля собрали по 38 ц пшеницы, а с каждогогектара второго - по 32 ц Сколько...
miakakashka miakakashka  05.04.2021 18:14
3) 3(2x - 7) = 9; р с обьяснением​...
leyla210 leyla210  05.04.2021 18:14
Зарплата рабочего выросла с 900 крон до 1044 крон в месяц. На сколько процентов увеличилась зарплата рабочего?​...

Популярные вопросы