Как проверить коллинеарность векторов c и d, построенных по векторам a и b?
если a(1; -2; 5) b(3; -1; 0) c= 4a-2b d=-2a+b.

Question

Математика: Как проверить коллинеарность векторов c и d, построенных по векторам a и b? если a(1; -2; 5) b(3; -1; 0) c= 4a-2b d=-2a+b.

Dima1234567y · Answer

Два вектора коллинеарны, если их соответствующие координаты пропорциональны.

Найдём координаты вектора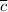 $\overline{c}$ :

$4\overline{a}=(1 \cdot 4, -2 \cdot 4, 5 \cdot 4)=(4,-8,20)\\-2\overline{b}=(-6, 2,0)\\\overline{c}=4\overline{a}+(-2 \overline{b})=(4-6, -8+2, 20+0)=(-2,-6,20)$

Далее найдём координаты вектора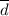 $\overline d$ :

$-2\overline a=(-2,4,-10)\\\overline b=(3,-1,0)\\\overline d=-2\overline a+\overline b=(-2+3,4-1,-10+0)=(1,3,-10)$

Разделим соответствующие координаты полученных векторов:

$-2:1=-2\\-6:3=-2\\20:(-10)=-2$

Видим, что координаты пропорциональны (коэффициент пропорциональности равен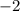 , то есть имеет место равенство 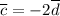$\overline c= -2 \overline d$ ). Следовательно, векторы коллинеарны.

Как проверить коллинеарность векторов c и d, построенных по векторам a и b? если a(1; -2; 5) b(3; -

Как проверить коллинеарность векторов c и d, построенных по векторам a и b? если a(1; -2; 5) b(3; -1; 0) c= 4a-2b d=-2a+b.

Популярные вопросы

Как проверить коллинеарность векторов c и d, построенных по векторам a и b?
если a(1; -2; 5) b(3; -1; 0) c= 4a-2b d=-2a+b.