1/2 arccos корень из 3/2 +1/3 arccos корень (-2/2)
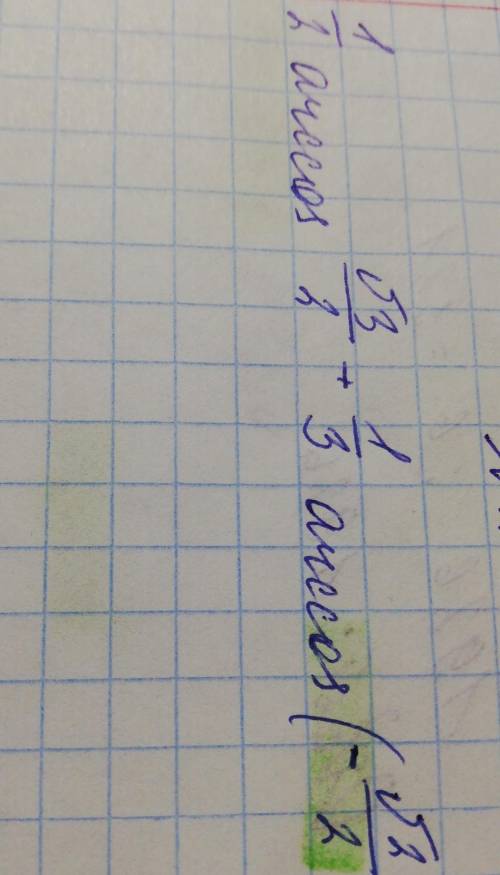
Другие вопросы по теме Математика
Популярные вопросы
- В борьбе за господство в Средиземноморье самый опасный противник Рима...
3 - Ваня прочитал 120 страниц что состовляет 4/11 всей книги вычисли сколько...
2 - Какие высказывания о климате Евразии являются верными? (Несколько вариантов...
3 - Дан равнобедренный треугольник abc с основанием ac, bm - биссектриса...
3 - Найти то,что требуется в таблице....
3 - В каком году был создан Союз писателей в МАССР?...
1 - Выбери наиболее вероятную последовательность появления групп организмов...
2 - 10-тапсырма.Махамбетке оқ атқан жігітті ақтауға бола ма?Оның қателесуі...
2 - ЕГЭ Русский язык 8 задание ...
1 - Коэффициент b в уравнения y=kx+b прказываетЧисловое значение или точку...
2
1/2 arccos корень из 3/2 +1/3 arccos корень (-2/2)
Разделим его на две части и рассмотрим каждую из них по отдельности.
Первая часть выражения: 1/2 arccos корень из 3/2
Для начала, нам нужно вычислить арккосинус корня из 3/2. Арккосинус - это обратная функция косинусу и обозначается как acos.
Мы знаем, что косинус это отношение прилежащей стороны к гипотенузе в прямоугольном треугольнике. Так как у нас корень из 3/2, мы можем представить это как прямоугольный треугольник с катетом 1 и гипотенузой sqrt(3).
Используя свойства тригонометрических функций, мы можем вычислить арккосинус sqrt(3/2).
arccos(sqrt(3/2)) = pi/6
Таким образом, первая часть выражения равна 1/2 * pi/6 = pi/12.
Теперь рассмотрим вторую часть выражения: 1/3 arccos корень (-2/2)
Аналогично первой части, нам нужно вычислить арккосинус корня (-2/2). Косинус - это отношение прилежащей стороны к гипотенузе в прямоугольном треугольнике. Так как у нас корень (-2/2), мы можем представить это как прямоугольный треугольник с катетом -1 и гипотенузой sqrt(2).
Так как у нас отрицательная сторона, мы можем представить это в виде угла, смещенного на pi радиан от исходного положительного угла. То есть арккосинус sqrt(2) равен pi - pi/4.
Используя свойства тригонометрических функций, мы можем вычислить arccos(sqrt(2)).
arccos(sqrt(2)) = pi/4.
Теперь мы можем рассчитать вторую часть выражения: 1/3 * pi/4 = pi/12.
Таким образом, исходное выражение можно записать как pi/12 + pi/12.
Чтобы сложить эти два выражения, нам нужно найти их общий знаменатель:
pi/12 + pi/12 = (pi + pi)/12 = 2pi/12 = pi/6
Итак, итоговый ответ на задачу равен pi/6.