1. Математика
  2. Избавьтесь от иррациональности

Избавьтесь от иррациональности в числители дроби и сравните ее с нулем

volkow2711ovuu5e volkow2711ovuu5e    2   03.11.2019 14:24    5

Ответы
Ксения200612 Ксения200612  10.10.2020 11:11

Пошаговое объяснение:

a) \frac{\sqrt[3]{3} - \sqrt[6]{12} }{2} =\frac{\sqrt[6]{9} - \sqrt[6]{12} }{2}

По формуле разности кубов

(\sqrt[6]{a})^3-(\sqrt[6]{b} )^3 = (\sqrt[6]{a} - \sqrt[6]{b})(\sqrt[6]{a^2} + \sqrt[6]{a} *\sqrt[6]{b} + \sqrt[6]{b^2})

\frac{\sqrt[6]{9} - \sqrt[6]{12} }{2}=\frac{(\sqrt[6]{9} - \sqrt[6]{12})(\sqrt[6]{9^2}+\sqrt[6]{9} * \sqrt[6]{12} +\sqrt[6]{12^2} )}{2(\sqrt[6]{9^2}+\sqrt[6]{9} * \sqrt[6]{12} +\sqrt[6]{12^2} )} =\frac{\sqrt{9} - \sqrt{12} }{2(\sqrt[6]{81}+\sqrt[6]{9} * \sqrt[6]{12} +\sqrt[6]{144} )} =

=\frac{(\sqrt{9} - \sqrt{12})(\sqrt{9} + \sqrt{12}) }{2(\sqrt[6]{81}+\sqrt[6]{9} * \sqrt[6]{12} +\sqrt[6]{144} )(\sqrt{9} + \sqrt{12})} =\frac{9-12}{2(\sqrt[6]{81}+\sqrt[6]{9} * \sqrt[6]{12} +\sqrt[6]{144} )(\sqrt{9} + \sqrt{12})} =

=\frac{-3}{2(\sqrt[6]{81}+\sqrt[6]{9} * \sqrt[6]{12} +\sqrt[6]{144} )(\sqrt{9} + \sqrt{12})}

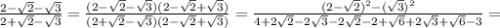
b) \frac{2-\sqrt{2} -\sqrt{3} }{2+\sqrt{2} -\sqrt{3}} =\frac{(2-\sqrt{2} -\sqrt{3} )(2-\sqrt{2} +\sqrt{3} )}{(2+\sqrt{2} -\sqrt{3})(2-\sqrt{2} +\sqrt{3} ) } =\frac{(2-\sqrt{2})^2-(\sqrt{3})^2}{4+2\sqrt{2} -2\sqrt{3}-2\sqrt{2}-2+\sqrt{6} +2\sqrt{3} +\sqrt{6}-3} =

Приводим подобные

=\frac{4-4\sqrt{2}+2-3}{2-3 +\sqrt{6} +\sqrt{6}} =\frac{3-4\sqrt{2}}{-1 +2\sqrt{6} }=\frac{(3-4\sqrt{2})(3+4\sqrt{2})}{(-1 +2\sqrt{6})(3+4\sqrt{2})} =\frac{9-32}{(-1 +2\sqrt{6})(3+4\sqrt{2})} =

=\frac{-23}{(-1 +2\sqrt{6})(3+4\sqrt{2})}

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
Tunior Tunior  26.05.2021 22:37
Как думаете, у парня большой ч*ен? Мне кажется, да…...
Артём00071 Артём00071  26.05.2021 22:35
Если в задании просят СТОРОНА ПИРАМИДЫ равна х это значит, что боковое ребро пирамиды равно х, или сторона основания равна х, или и то, и то тоже равно х?? УМОЛЯЮ ЗНО...
ShudrenkoArtem ShudrenkoArtem  26.05.2021 22:35
Зробіть будь ласка 4, 5, 6 завдання...
ALXEN03 ALXEN03  26.05.2021 22:34
(2x-7) (9-4x)=0 НУЖНО ДО ЗАВТРА ДО 13:15 И РЕШЕНИЕ ​...
Mojo228 Mojo228  26.05.2021 22:34
Розвязать уравнение : 1) х-2 = 5 32 122) 4 = 36 3х-11 63(если что цифри в низу это дробь)...
alskyuq alskyuq  26.05.2021 22:33
Стоимость 4 тетрадей и 3 карандашей 3300 сум, Стомость 1 и 2 карандашей 1200 сум Найдите стоимость 1 тет. и 1 кар. С ОБЬЯСНЕНИЯМ ​...
Daya98888888 Daya98888888  26.05.2021 22:32
На вечеринке есть три вида напитков: сок, вода и газировка. Известно, что сок выпили 20 человек. Количество тех, кто ВЫПИЛ воду составляет 4/5 количества тех, кто выпил...
Абухассан Абухассан  26.05.2021 22:31
отношение двух чисел равно 1/6 найди эти положительные числа,если их разность равна 0,75. Меньшее число равно. Большее число равно.​...
bobrovnikova13 bobrovnikova13  26.05.2021 22:28
Четверо робітників виготовили 152 деталі. Другий 5 робітник виготовив кількості деталей, виготовле- 6 них першим, третій -- 90 % того, що виготовив другий, а четвертий...
оооооаомт оооооаомт  26.05.2021 22:27
За 6 кг мармеладу заплатили стільки, скільки за 3,6 кг шоколадних цукерок. Яка ціна кожного виду цукерок, якщо 1 кг мармеладу дешевший від 1 кг шоколадних цукерок на...

Популярные вопросы