Из натуральных чисел от 1 до 100 выбрали 10 чисел. Докажите, что
можно составить из них два набора с одинаковой суммой (одно число можно ис-
пользовать не более одного раза; возможно, какие-то числа останутся неисполь-
зованными).

Рассмотрим все возможные непустые наборы, состоящие из каких-то из 10 выбранных чисел. Таких наборов 1023: каждое число можно независимо взять или не взять в набор, это даст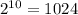 вариантов, и 1 вариант, когда набор пустой, нужно исключить.

Выпишем сумму чисел каждого из таких наборов. Максимальное возможное выписанное значение , так что различных возможных сумм не больше 955. Поскольку мы выписали 1023 суммы, значит, какие-то два набора имеют одинаковую сумму.

Из каждого из найденных наборов исключим числа, входящие в оба набора (если такие числа есть, конечно). Суммы чисел останутся равными, поскольку обе суммы уменьшились на одно и то же число; получившиеся наборы будут непусты (ни один набор не может полностью входить в другой, иначе их суммы были бы не равны).

Итак, мы получили, что нашлись два набора, содержащие разные числа, имеющие одинаковые суммы. Ура!