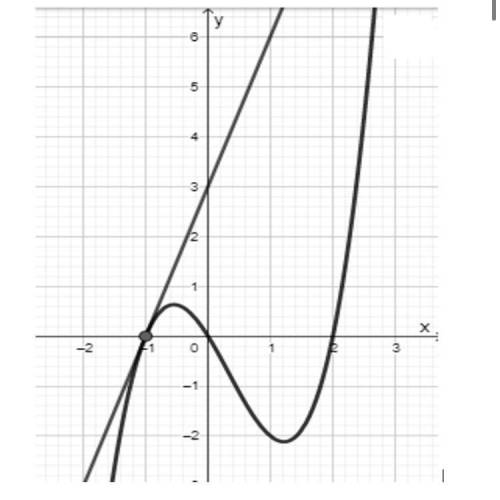
Хлп Отметить вопрос на рисунке изображен график функции F(x) и график этой функции, проведенный в точке (-1; 0). определите значение f' (-1)
a)3
B)1
C)2
D)-1
E)0
Другие вопросы по теме Математика
Популярные вопросы
- 1) Какие из чисел: 114, 116, 132, 143, 372, 438, 647 делятся на 6. Выпишите...
1 - Найдите площадь округа . 1) R=2 см 2) R=5 см 3) D=4 см...
3 - Ский язык School life and classes. (Round up) (Школьнаяжизнь и занятия)Write...
2 - Что объединяет Чудинова и Наташу Скуратову...
3 - 1.По уравнению движения определите: координату точки в начальный момент...
3 - Дано m(H2)=1 г m(O2)=1г m(ост.вещ-ва)-?...
2 - Воспитатель: Дорогие дети, добро в наш ботанический сад - одно из самых...
3 - Мәтіннің басты кейіпкері не істеді? Алмас күнде таңертең тұрып, Мәдениет...
1 - Какая сила заставляет оболочку шарика расходится в разные стороны...
3 - определите расстояние от Ташкента до индийского и Атлантического и Северно...
3
Для начала, давайте разберемся с графиком функции F(x). Из рисунка видно, что функция имеет возрастающий участок на интервале (-∞, -1) и убывающий участок на интервале (-1, ∞).
Теперь посмотрим на график этой функции, проведенный в точке (-1, 0). Мы видим, что график функции пересекает ось x в точке (-1, 0), что означает, что функция F(x) в точке (-1) равна 0.
Мы хотим найти значение производной функции f'(-1). Производная функции показывает скорость изменения функции в каждой точке. В данном случае, мы хотим узнать скорость изменения функции F(x) в точке (-1).
Из графика видно, что на участке функции F(x), где x находится слева от точки (-1), функция возрастает. Значит, производная функции f'(x) будет положительной в этом участке.
С другой стороны, на участке функции F(x), где x находится справа от точки (-1), функция убывает. Значит, производная функции f'(x) будет отрицательной в этом участке.
Поскольку график функции F(x) пересекает ось x в точке (-1, 0), мы можем сделать вывод, что производная функции f'(-1) равна 0.
Таким образом, ответ на вопрос "определите значение f'(-1)" равен E) 0.