Довести, що відношення периметра трикутника до однієї із його сторін
дорівнює відношенню висоти, яка проведена до цієї сторони, до радіуса
вписаного кола.

Доказать, что отношение периметра треугольника к одной из его сторон
равен отношению высоты, проведенной к этой стороне, к радиусу
вписанной окружности.​

Рисунок рисовать даже необязательно. Введем следующие числовые параметры: пусть - одна из сторон произвольного треугольника, 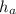- сторона, проведенная к этой стороне; 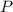- периметр треугольника; - радиус вписанной окружности.

Запишем формулы для вычисления площади треугольника:

,     ⇒ .

Отсюда следует, что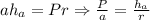 , что и требовалось доказать.