Докажите, что для любых множеств A, B, C
(A∩B)∪C=(А∪С)∩(В∪С);

Другие вопросы по теме Математика
Популярные вопросы
- Сколько литров воды уравновесили бы весы, на одной чаше которых...
1 - В ТЕАТРЕ Мне было лет восемь, когда старшая сестра взяла мены с...
2 - Listen to the recording and choose the best answer. The main subject...
3 - Написать 10 слов на адгейсском языке, показывающие черту характера...
2 - Всем привет привет найти ответы 10 класс?...
3 - От каких особенностей передачи зависит выбор коэффициента ψba при...
1 - Що таке право вето,у яких випадках і ким воно застосовувалось?...
3 - У подножия горы температура +3 градуса. Какая температура будет...
1 - 1.Один из углов прямоугольного треугольника равен 30°, сумма гипотенузы...
3 - (написать продолжение рассказа «Багульник» - 5-10 предложений)...
2
Поучительным подходом будет использование характеристической функции.
Характеристическая функция множества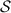 берет на вход некоторый элемент (универсального множества) и возвращает 1, если этот элемент принадлежит
берет на вход некоторый элемент (универсального множества) и возвращает 1, если этот элемент принадлежит 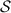 , и 0 в противном случае.
, и 0 в противном случае.
Иными словами,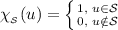 .
.
Исходя из этого,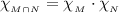 . Понятно, что
. Понятно, что 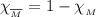 , поэтому
, поэтому 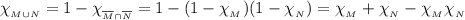 (первый переход опирается на правило де Моргана).
(первый переход опирается на правило де Моргана).
Возьмем характеристическую функцию от двух частей равенства. Слева: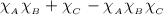 . Справа:
. Справа: 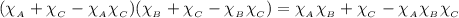 (убедитесь сами: понятно, что
(убедитесь сами: понятно, что 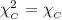 ), что и доказывает требуемое.
), что и доказывает требуемое.