Докажите, что для любого натурального числа n, найдутся две различные степени числа 7, разность которых кратна n.
Ответы
Здесь надо делать по теореме Эйлера, которая говорит, что если а и m взаимно просты, то 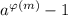 всегда делится на m. Здесь
всегда делится на m. Здесь 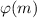 - функция Эйлера, которая равна количеству натуральных чисел не превосходящих m и взаимно простых с m. Если это использовать, то решение такое.Число n всегда можно записать в виде
- функция Эйлера, которая равна количеству натуральных чисел не превосходящих m и взаимно простых с m. Если это использовать, то решение такое.Число n всегда можно записать в виде 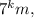 где k≥0, m≥1 и m взаимно просто с 7. Тогда по теореме Эйлера число
где k≥0, m≥1 и m взаимно просто с 7. Тогда по теореме Эйлера число 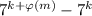 делится на n, т.к. оно равно
делится на n, т.к. оно равно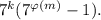
ПОКАЗАТЬ ОТВЕТЫ
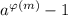 всегда делится на m. Здесь
всегда делится на m. Здесь 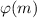 - функция Эйлера, которая равна количеству натуральных чисел не превосходящих m и взаимно простых с m. Если это использовать, то решение такое.Число n всегда можно записать в виде
- функция Эйлера, которая равна количеству натуральных чисел не превосходящих m и взаимно простых с m. Если это использовать, то решение такое.Число n всегда можно записать в виде 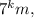 где k≥0, m≥1 и m взаимно просто с 7. Тогда по теореме Эйлера число
где k≥0, m≥1 и m взаимно просто с 7. Тогда по теореме Эйлера число 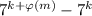 делится на n, т.к. оно равно
делится на n, т.к. оно равно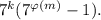
Другие вопросы по теме Математика
Популярные вопросы
- I. Запишите текст, подчеркните грамматические основы предложений. Составьте...
3 - Позначте цифрами правильну відповідь Дія, сформована шляхом повторення,...
3 - Вычислить значения выражений...
3 - Ротовой опорат у неандертальца...
1 - Город Москва(560 с.ш. 370 в.д.) расположена от столицы Индии Дели (290 с.ш....
3 - 3.Правила проведения экзамена. 4 Отчёт о проделанной работеРусский язык...
2 - К какому типу односоставных предложений относится чувство языка надо ценить...
1 - надо написать названия по картинкам все...
1 - 5 - тапсырма . « Күлтегін » ескерткіші жайында сөйлеу тілінде және ресми...
3 - Речення зі словом мобільник...
1