Докажите, что число 3 ¹⁰⁰+ 1 делится на 2; б) число 9²⁰⁰⁰ – 7²⁰⁰⁰ на 10.​

При возведении нечётного числа в любую степень получим нечётное число. Если прибавить к нему единицу, число станет чётным (нечёт + нечёт = чёт).

----------------

Число 10 делится на 2 и на 5. Надо доказать, что наше число делится и на 2, и на 5. Разложим его по формуле разности квадратов:

Докажем, что множитель делится на 10 (если один из множителей числа делится на 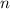, в данном случае на 10, то и всё число делится на )

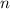Число, которое оканчивается на 1, в любой степени оканчивается на 1, поэтому разность данных чисел оканчивается на нуль. Это признак деления на 10.

1) 3 в любой степени - нечетное число. Если прибавить 1, то получится четное, а значит делится на 2 - ч.т.д.

Можно привести доказательство в общем виде:

Чтобы число делилось на два, нужно чтобы последняя цифра этого числа была 0; 2; 4; 6 или 8

Проверим на какие цифры заканчивается 3 в натуральной степени

1) 3¹=3

2) 3²=9

3) 3³=...7

4) 3⁴=...1

5) 3⁵=...3

Начиная с пункта 5) цифры будут повторятся (3,9,7,1,3,9,7,1,3 и т.д.).

Как видим, все числа получаются нечетные, значит если к ним прибавить 1, то получатся цифры на конце 4; 0; 8; 2 то есть полученное число будет четным и поделится на 2 - ч.т.д.

2) Посмотрим на что оканчивается 9 в натуральной степени:

1) 9¹=9

2) 9²=...1

3) 9³=...9

Период повтора равен 2

Чтобы узнать на какую цифру оканчивается число 9²⁰⁰⁰ нужно 2000 поделить на период.

Если получится остаток, то смотрим на соответствующий пункт, если остатка нет, то смотрим на последний пункт периода

2000:4=500 (остаток 0)

Значит последняя цифра будет такая же как и 2) 9²=...1

Посмотрим на что оканчивается 7 в натуральной степени:

1) 7¹=7

2) 7²=...9

3) 7³=...3

4) 7⁴=...1

5) 7⁵=...7

Период 4

2000:4=500 (остаток 0)

Значит цифра на конце такая же как и 4) 7⁴=...1

Тогда

9²⁰⁰⁰-7²⁰⁰⁰=...1-...1=...0 - число оканчивается на 0, значит оно делится на 10 - ч.т.д.