Доказать гипотезу Римана: «Все нетривиальные нули дзета-функции имеют действительную часть, равную »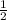

Дзета-функция Римана — функция \displaystyle \zeta (s) комплексного переменного s=\sigma +it, при \sigma >1 определяемая с ряда Дирихле:

\zeta (s)={\frac {1}{1^{s}}}+{\frac {1}{2^{s}}}+{\frac {1}{3^{s}}}+\ldots ,
где \displaystyle s\in \mathbb {C}

вниомаомылт    3   04.12.2020 07:26    2