Доказать, что данное выражение является полным дифференциалом некоторой функции u=(x,y) и найти эту функцию.
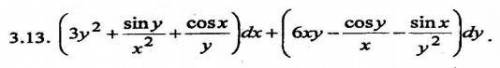
Другие вопросы по теме Математика
Популярные вопросы
- Поставить тире в предложениях.книга мой лучший друг. художник и.шишков любил рисовать...
1 - Мальвина написала на доске верное равенство. буратино переписал его в тетрадку...
2 - Найти 15 словосочетаний из произведения а.с.пушкина капитанская дочь...
3 - Морфемный разбор слова загрустить, заночевать...
3 - Впределах зоны сильных землетрясений находится 1 остров сахалин 2 кольский полуостров...
2 - Плато путорана расположено в пределах: а)пояса гор южной сибири б)среднесибирского...
3 - Вычислите используя распределительное свойство 90*15+10*15 150*40-149*40...
3 - Написать 10 предложений на тему моя школьная жизнь...
2 - Прикладные программы для выполнения на компьютере конкретных ?...
1 - На какие две группы делятся члены предложения ?...
2
P(x;y)dx+Q(x;y)dy
является полным дифференциалом, если
∂P/∂y=∂Q/∂x.
∂P/∂y=((x+y)/(xy))`y=((x+y)`y·(xy)–(xy)`y·(x+y))/(xy)2= –x2/(xy)2= – 1/y2
∂Q/∂x=(1/y2)·(y–x)`x=(1/y2)·(–1)=–1/y2
∂P/∂y=∂Q/∂x
Данное уравнение – уравнение в полных дифференциалах
Это значит
∂U/∂x=P(x;y)
∂U/∂y=Q(x;y)
Зная, частные производные можем найти U(x;y)
U(x;y)= ∫ (∂U/∂x)dx= ∫ P(x;y)dx= ∫ (x+y)dx/(xy)=
=(1/y) ∫ (x+y)dx/x=(1/y) ∫ (1+(y/x))dx=(1/y)·x+(1/y)·yln|x|+ φ (y)=
=(x/y)+ln|x|+ φ(y)
Находим
∂U/∂y= ((x/y)+ln|x|+ φ(y))`y=x·(1/y)`+0+ φ `(y)= (–x/y2)+φ `(y)
Так как
∂U/∂y=Q(x;y)
то
(–x/y2)+φ `(y) =(y–x)/y2;
⇒
φ `(y)=1/y
φ(y)=ln|y|+C
U(x;y)=(x/y)+ln|x|+ φ(y)=(x/y)+ln|x|+ln|y|+C
О т в е т.U(x;y)=(x/y)+ln|x·y|+C