Дифференциальное исчисление функции одной переменной xy+ln(y)-2ln(x)=0 , y'x - ?
На картинке понятнее
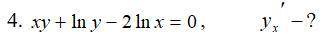
Другие вопросы по теме Математика
Популярные вопросы
- Две небольшие лодки закреплены посередине быстрой реки с веревок, которые тянутся...
1 - Сваю массой 100 кг забивают в грунт копром, масса которого 400 кг. Копер свободно...
3 - При подготовке игрушечного пистолета к выстрелу пружину жесткостью 800 Н/м сжали...
3 - Электропоезд в момент выключения тока имел скорость 20 м/с. Какой путь пройдет...
2 - Тело брошено со скоростью 20 м/с под углом 30° к горизонту. Определите его скорость...
2 - С какой начальной скоростью v0 надо бросить вниз мяч с высоты 2 м, чтобы он...
3 - Тело с начальной скоростью 14 м/с падает с высоты 240 м и углубляется в песок...
2 - Хоккейная шайба скользит 5 м, если при броске ей сообщают начальную скорость...
3 - Начальная скорость пули 600 м/с, ее масса 10 г. Под каким углом к горизонту...
1 - Автомобиль массой 2 т затормозил и остановился, пройдя путь 50 м. Найдите работу...
3
Находим частную производную по х: