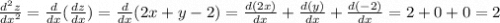Дифференциальное исчисление функции нескольких переменных. Задание на скриншотах.

Другие вопросы по теме Математика
Популярные вопросы
- В ящике 5 желтых, 4 фиолетовых и 3 розовых фломастера. Наудачу вынимают...
3 - Будущее время глагола Укажите глагол, стоящий в форме будущего времени....
3 - На координатной прямой точке N соответствует число c+4, а точке D — число...
3 - В схеме приборы показывают ток 0,1 А, U1= 30В U2= 120В U3= 80В. Определить...
2 - Назовите основные признаки второстепенных членов. Расставьте знаки препинания...
1 - Вигнання з України нацистських окупантів Роздивитися 6 (шосте) ФОТО уважно...
2 - Английский язык интерактивная тетрадь skysmart заполните пропуски с фотки...
3 - 2. Раз так много похожего, от чего тогда зависело, кто станет лидером...
2 - Синтаксический разбор предложения Появление скворцов - признак близкой...
2 - Г. Перечитай эпизод о псаре и барашке, которого он нашел. Придумай продолжение....
2
1)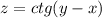 :
:
а)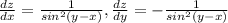
б)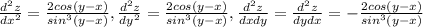
2)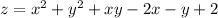 :
:
а)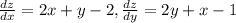
б)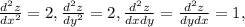
Пошаговое объяснение:
Частная производная — это предел отношения приращения функции по выбранной переменной к приращению этой переменной, при стремлении этого приращения к нулю.
1)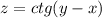 :
:
а)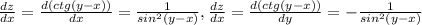
б)
2)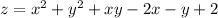 :
:
а)
б)