Даны векторы a (6; -3; 6) и b (4; -2; 5) Найти косинус угла между векторами 1/3b и 3a.
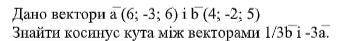
Другие вопросы по теме Математика
Популярные вопросы
- 1.Кто открыл явления фагоцитоза? 2. Как называется клетки крови участвующие...
2 - Не на что жить, как не скатиться окончательно в канаву?...
3 - Що значить ДРАКОТТО ПОКОРРІ?...
2 - Радіус основи конуса дорівнює 12см а кут при вершині осьового перерізу...
2 - По какой причине вассал мог быть лишен земли? а.если он переставал...
3 - Прокоментуйте слова воїнів Бертольда «Краще смерть, ніж вічний сором»....
3 - Очень КРАТКО И Материки Значение средней плотности населения (чел\км2...
2 - Ребят Что делать??? Мне нужно открыть работу, которая скоро закроется...
3 - Дослідіть, які корисні копалини використовує промисловість для забезпе...
1 - Задача на акустический расчет по защите от шума Не понимаю как делать...
2
Пошаговое объяснение:
сперва сосчитаем вектора
1/3 b (4/3; -2/3; 5/3
3a (18; -9;18)
скалярное произведение
a*b = (18 *4 /3) + (-9)* (- 2/3) + (18 *5/ 3) = 24 + 6 + 30 = 60
теперь найдем длины векторов
= √(324 + 81 + 324) = √729 = 27
|b| = √(16/9 + 4/9 + 25/9) = √5
и косинус угла