Математика: Даны точки a(-1; 2; 4), b(3; 0; -1), c(2,6,1). найти угол b

Даны точки a(-1; 2; 4), b(3; 0; -1), c(2,6,1). найти угол b

Ответы

Анжелика200611111 10.10.2020 23:04

$\alpha = arccos(\frac{26}{3\sqrt{205}})$

Пошаговое объяснение:

Обозначим за α угол ABC;

Найдем векторы BA и BC:

BA = (-4, 2, 5); BC = (-1, 6, 2).

Скалярное произведение этих векторов находится как сумма произведений соответственных координат:

(BA, BC) = (-4) * (-1) + 2 * 6 + 5 * 2 = 4 + 12 + 10 = 26. С другой стороны, по определению скалярного произедения векторов (BA, BC) = |BA| * |BC| * cos(α). Тогда $cos(\alpha) = \frac{(BA, BC)}{|BA|*|BC|} = \frac{26}{\sqrt{16 + 4 + 25} * \sqrt{1 + 36 + 4}} = \frac{26}{3\sqrt{205}}$ .

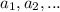Чтобы определить знак угла α, можно было бы найти еще и sin(α), используя "формулу" (в виде определителя она записывается для удобства, но, вообще говоря, такая запись не вполне корректна) $[a,b] = det\left[\begin{array}{ccc}i&j&k\\a_{1}&a_{2}&a_{3}\\b_{1}&b_{2}&b_{3}\end{array}\right]$ , где [a, b] - векторное произведение векторов a и b, $a_{1}, a_{2}, ...$ - координаты векторов a и b, а i, j, k - базисные векторы. Но т.к. знак угла между данными векторами нам не важен, то мы можем сразу дать ответ: