Диагонали трапеции равны 10 см и 12 см. найдите периметр четырёхугольника, вершинами которого являются середины сторон данной трапеции.

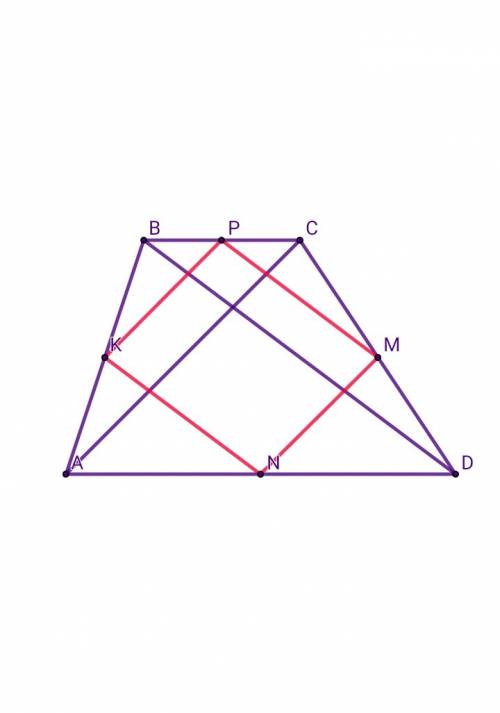
Пусть К, Р, M, N - середины сторон соответственно АВ, BC, CD, AD, тогдаВ ΔABD: AK = KB, AN = ND ⇒ KN - средняя линия" Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны "KN || BD, KN = BD/2В ΔBCD: BP = PC, CM = MD ⇒ PM - средняя линияPM || BD, PM = BD/2Значит, KN || PM , KN = PMИз этого следует, что четырёхугольник KPMN - параллелограмм (по признаку параллелограмма)KN = BD/2 , KP = AC/2Р kpmn = 2•(KN + KP) = 2•(BD/2 + AC/2) = BD + AC = 12 + 10 = 22 смОТВЕТ: Р = 22 см