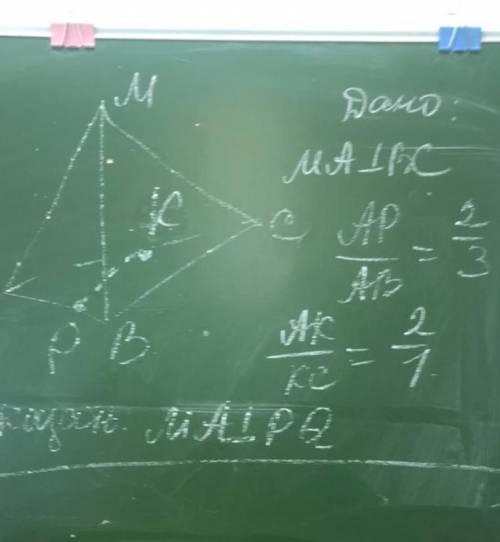
дан тетраэдр MABC, в нем MA перпендикулярно BC. AP /АВ= 2/3. АК/КС=2/1 доказать что МА перпендикулярно РК​

Чтобы доказать, что MA перпендикулярно РК, мы можем воспользоваться свойствами параллелограмма и пропорциями.

1. Рассмотрим параллелограмм АСПК. В нем угол РАК равен углу СПК (соответственные углы при параллельных прямых). Кроме того, угол РКС также равен углу АКП (внешний угол параллелограмма).

2. По условию, AP / АВ = 2/3 и АК / КС = 2/1. Мы можем применить свойство делящей густоты: если отрезок делится двумя отрезками так, что отношение длин первого отрезка к длине второго совпадает с отношением длин второго отрезка к длине третьего, то эти отрезки делятся в одной точке пополам.

3. Таким образом, отношение длин отрезка АП к отрезку РК будет равно отношению длин отрезка АВ к отрезку КС. Исходя из условия, у нас получается следующее соотношение: АП / РК = АВ / КС = 2/3.

4. Так как у нас параллелограмм АСПК, то углы РАК и СПК равны. Кроме того, у нас также есть равенство углов АКП и РКС. Используем свойство параллелограмма: если противоположные стороны параллельного четырехугольника равны, то противоположные углы равны.

5. У нас получается, что углы РАК и АКП равны, а также СПК и РКС равны. То есть, у нас получается, что углы РАК и АКП равны углам СПК и РКС.

6. Исходя из свойства равных углов, мы можем сделать вывод, что треугольники AMP и KRP подобны. Это означает, что их соответственные стороны пропорциональны друг другу.

7. Так как стороны AM и KR соответственны в пропорции АП / РК = АВ / КС = 2/3, то мы можем сказать, что сторона AM в два раза больше стороны KR, так как АП в два раза больше РК (пропорция 2/3).

8. Следовательно, длина отрезка MA в два раза больше длины отрезка RK. При этом у нас совпадают направления этих отрезков, так как MA и RK находятся в одной плоскости. Значит, отрезки MA и RK должны быть перпендикулярны друг другу.

Таким образом, мы доказали, что MA перпендикулярно RK.