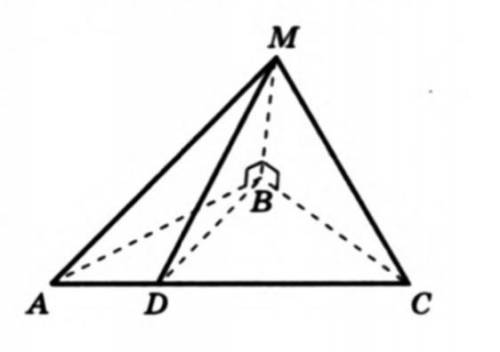
Дан тетраэдр MABC, в котором MB перпендикулярен BC, MB перпендикулярен BA. 1. Докажите, что треугольник MDB прямоугольный, если D - произвольная точка отрезка AC.
2. Найдите MD и площадь треугольника MBD, если MB=BD=2.

Для решения задачи нам потребуются несколько геометрических свойств и определений:

1. Определение прямоугольного треугольника: треугольник называется прямоугольным, если у него есть один прямой угол (90 градусов).

2. Теорема о перпендикулярных прямых: если две прямые AB и CD перпендикулярны друг другу, то все углы, образованные этими прямыми, будут прямыми.

Теперь давайте решим задачу:

1. Докажем, что треугольник MDB является прямоугольным.

У нас есть два условия: MB перпендикулярен BC и MB перпендикулярен BA.

Давайте проведем прямую MD, исходящую из точки D, перпендикулярно AC. Обозначим точку пересечения этой прямой с BC как E.

Теперь вспомним теорему о перпендикулярных прямых: если прямая MB перпендикулярна BC, а прямая MD перпендикулярна AC, то угол MDB будет прямым (90 градусов).

Таким образом, мы доказали, что треугольник MDB является прямоугольным для любой произвольной точки D на отрезке AC.

2. Найдем MD и площадь треугольника MBD, если MB=BD=2.

У нас уже есть прямоугольный треугольник MDB. Известно, что MB=BD=2.

Так как MB и BD равны, то треугольник MBD является равнобедренным.

Из свойств равнобедренного треугольника мы знаем, что высота, опущенная из вершины угла между равными сторонами, является медианой, биссектрисой и высотой одновременно.

Таким образом, медиана MD является высотой треугольника MBD.

Мы можем использовать теорему Пифагора для нахождения длины медианы MD:

MD^2 = MB^2 - BD^2 = 2^2 - 2^2 = 4 - 4 = 0

Отсюда следует, что MD = 0.

Теперь найдем площадь треугольника MBD.

Площадь треугольника можно найти, используя формулу для площади треугольника по высоте и основанию:

Площадь MBD = (основание MBD * высота MD) / 2 = (2 * 0) / 2 = 0.

Таким образом, мы получаем MD = 0 и площадь треугольника MBD = 0.

Суммируя наши результаты, мы доказали, что треугольник MDB является прямоугольным, MD = 0 и площадь треугольника MBD = 0 при условии MB=BD=2.