DABC - правильная треугольная пирамида. Сторона основания равна 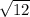. Боковые ребра наклонены к основанию под углом 60°. Найдите |CB + AD + BA| (CB, AD, BA - векторы). Приложите решение.

Для нахождения значения выражения |CB + AD + BA| нам нужно сначала вычислить каждый из векторов CB, AD и BA, а затем сложить их и вычислить длину полученного вектора.

Для начала, давайте посмотрим на треугольник CDB, который образуется боковым ребром треугольной пирамиды DABC. Этот треугольник является прямоугольным, так как его сторона BD является высотой пирамиды, а угол CDB равен 90°.

По условию, мы знаем, что угол между боковыми ребрами и плоскостью основания равен 60°. Так как основание треугольной пирамиды DABC является правильным треугольником, то угол между стороной основания и боковым ребром (то есть угол CBD или CDB) также равен 60°.

Далее, мы можем использовать тригонометрию для нахождения значений сторон треугольника CDB. Так как сторона основания треугольной пирамиды равна √12, то стороны треугольника CDB будут равны:

CD = √12 sin 60° = √12 * √3/2 = √36/2 = 3

BD = √12 cos 60° = √12 * 1/2 = √12/2 = √3

Теперь, давайте рассмотрим треугольник ABD. Мы уже знаем, что сторона BD равна √3. Также, сторона AB является стороной основания треугольной пирамиды, которая также равна √12.

Используя теорему Пифагора, мы можем найти значение стороны AD:

AD² = AB² - BD²
AD² = (√12)² - (√3)²
AD² = 12 - 3
AD² = 9
AD = 3

Теперь наша задача состоит в том, чтобы найти векторы CB, AD и BA и сложить их.

CB - вектор, соединяющий точку C с точкой B.
AD - вектор, соединяющий точку A с точкой D.
BA - вектор, соединяющий точку B с точкой A.

Сначала давайте найдем вектор CB. Вектор CB можно найти, вычитая координаты точки C из координат точки B:

CB = (x_B - x_C, y_B - y_C, z_B - z_C)

Здесь (x_C, y_C, z_C) - координаты точки C, а (x_B, y_B, z_B) - координаты точки B.

Однако, так как в задаче нет конкретных значений координат точек C и B, мы не можем найти точные значения вектора CB. Мы можем только записать его в виде:

CB = (x_B - x_C, y_B - y_C, z_B - z_C)

Аналогично, давайте найдем вектор AD.

AD = (x_D - x_A, y_D - y_A, z_D - z_A)

Здесь (x_D, y_D, z_D) - координаты точки D, а (x_A, y_A, z_A) - координаты точки A.

Опять же, так как в задаче нет конкретных значений координат точек D и A, мы не можем найти точные значения вектора AD. Мы можем только записать его в виде:

AD = (x_D - x_A, y_D - y_A, z_D - z_A)

Наконец, давайте найдем вектор BA.

BA = (x_A - x_B, y_A - y_B, z_A - z_B)

Здесь (x_A, y_A, z_A) - координаты точки A, а (x_B, y_B, z_B) - координаты точки B.

Аналогично, без конкретных значений координат точек A и B, мы можем только записать вектор BA в виде:

BA = (x_A - x_B, y_A - y_B, z_A - z_B)

Теперь, чтобы найти значение выражения |CB + AD + BA|, мы должны сложить каждую из компонент векторов CB, AD и BA:

CB + AD + BA = (x_B - x_C, y_B - y_C, z_B - z_C) + (x_D - x_A, y_D - y_A, z_D - z_A) + (x_A - x_B, y_A - y_B, z_A - z_B)

Заметим, что некоторые компоненты векторов сократятся:

CB + AD + BA = (- x_C + x_A + x_D - x_B, - y_C + y_A + y_D - y_B, - z_C + z_A + z_D - z_B)

Следовательно, значение выражения |CB + AD + BA| равно длине полученного вектора:

|CB + AD + BA| = √((- x_C + x_A + x_D - x_B)² + (- y_C + y_A + y_D - y_B)² + (- z_C + z_A + z_D - z_B)²)

Однако, так как у нас отсутствуют конкретные значения координат точек C, B, D и A, нам невозможно найдти точное значение длины полученного вектора.