Проверить что четыре точки а(3; -1; 2) в(1; 2; -1) с(-1; 1; -3) d(3; -5; 3) служат вершинами трапеции

Ответы

rizakovaarina 06.10.2020 23:30

Пошаговое объяснение:

Трапецией называется четырехугольник, у которого одна пара противоположных сторон параллельна, и стороны не равны между собой.

Для проверки этих условий вычислим векторы:

АВ=(1-3;2-(-1);-1-2)=(-2;3;-3)

ВС=(-1-1;1-2;-3-(-1))=(-2;-1;-2)

CD=(3-(-1);-5-1;3-(-3))=(4;-6;6)

DA=(3-3;-1-(-5);2-3)=(0;4;-1)

Теперь проверим вычисленные векторы на коллинеарность. Этого достаточно для вывода о параллельности, т.к. координаты точек не совпадают.

Два вектора a и b коллинеарны, если существует число n такое, что

а=n×b.

Как видно из координат векторов, таких вектора у нас 2: АВ и CD, т.к.

АВ×(-2)=СD.

Теперь проверим условие, что длины сторон (т.е. векторов) не равны между собой.

|AB|=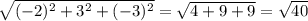 $\sqrt{(-2)^{2}+3^{2}+(-3)^{2} } =\sqrt{4+9+9} =\sqrt{40}$

|BC|=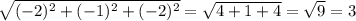 $\sqrt{(-2)^{2}+(-1)^{2}+(-2)^{2} } =\sqrt{4+1+4} =\sqrt{9} =3$

|CD|=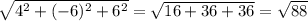 $\sqrt{4^{2} +(-6)^{2}+6^{2} } =\sqrt{16+36+36} =\sqrt{88}$

|DA|=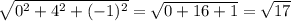 $\sqrt{0^{2}+4^{2}+(-1)^{2} } =\sqrt{0+16+1} =\sqrt{17}$

Как видим, ни один из векторов не имеет одинаковую длину с каким-либо другим из четырёх имеющихся.

Все условия соблюдены. Значит АВСD - трапеция.

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Математика

KarinaBelous 10.04.2020 21:04

1. 0,8( 3a-14)-0,6(6a-8), якщо a=-три ціліх . одна дванадцята...

ElenaScience 10.04.2020 21:04

jiohjb 10.04.2020 21:03

ralibaev 10.04.2020 21:03

До ть скласти і розв язати задачу за схемою ...

gymnazium006 10.04.2020 21:03

55555Даша11111111111 10.04.2020 21:03

Вика2003033 10.05.2020 11:30

vitalii1962svet 10.05.2020 11:30

Вандализм 10.05.2020 11:30

Kiri205 10.05.2020 11:31