Чему равен sin (a+a), если sin (a) - cos (a) = 0,7?
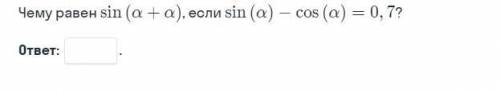
Другие вопросы по теме Математика
Популярные вопросы
- Определите температуру газа,находящегося в закрытом ,если его давление...
2 - Визнач відмінок іменників,звертаючи увагу на їх закінчення.спиши, ставляючи...
1 - Что случилось бы, если исчезли источники, колодцы и что мы делаем в этой...
3 - Прочитайте стихотворение пушкина дорожные жалобы . можно ли отнести его...
2 - Запишите в виде бесконечной переодической десятичное дроби частное: 1)...
1 - Во сколько идет передача урок на канале культура ? там где отец объясняет...
3 - как изменилась политич. структура европы после победы над наполеоном?...
1 - Ккакому функциональному стилю относится этот текст? периодически осматривать...
1 - Сочинение на тему сила трения в ходьбе - 7 кл...
3 - Сравни мир,в котором живет царь солтан,и мир,в котором существует его...
1
ответ: sin( α + α ) = sin2α = 0,51 .
Пошаговое объяснение:
# sinα - cosα = 0,7 ; пінесемо до квадрата :
sin²α - 2sinαcosα + cos²α = 0,7² ;
( sin²α + cos²α ) - 2sinαcosα = 0,49 ;
1 - sin2α = 0,49 ;
sin2α = 1 - 0,49 ;
sin2α = 0,51 .
Дано уравнение sin(a) - cos(a) = 0,7.
Для начала, нам понадобится выразить sin(a+a) через sin(a) и cos(a). Мы можем использовать формулу двойного угла для синуса:
sin(2t) = 2sin(t)cos(t).
Заменим 2t на a+a:
sin(a+a) = 2sin(a)cos(a).
Теперь у нас есть два уравнения: sin(a) - cos(a) = 0,7 и sin(a+a) = 2sin(a)cos(a).
Используя первое уравнение, мы можем выразить sin(a) через cos(a):
sin(a) = cos(a) + 0,7.
Теперь подставим это выражение во второе уравнение:
sin(a+a) = 2(cos(a) + 0,7)cos(a).
Раскроем скобки и упростим:
sin(a+a) = 2cos^2(a) + 1,4cos(a).
Однако, нам необходимо найти конкретное численное значение sin(a+a). Для этого нам понадобится дополнительная информация.
Искомое значение sin(a) - cos(a) = 0,7.
Мы знаем, что sin^2(a) + cos^2(a) = 1 (тождество Пифагора).
Теперь мы можем использовать это соотношение для решения уравнения:
(sin(a) - cos(a))^2 + cos^2(a) = 1.
Раскрываем квадрат и упрощаем:
sin^2(a) - 2sin(a)cos(a) + cos^2(a) + cos^2(a) = 1.
Сокращаем подобные члены:
2cos^2(a) - 2sin(a)cos(a) = 0.
Делим уравнение на 2cos(a):
cos(a) - sin(a) = 0.
Таким образом, мы получаем новое уравнение cos(a) - sin(a) = 0, которое в точности равно sin(a) - cos(a) = 0,7.
Теперь мы можем использовать это уравнение для решения задачи.
Подставим sin(a) = cos(a) + 0,7 в уравнение cos(a) - sin(a) = 0:
cos(a) - (cos(a) + 0,7) = 0.
Упростим:
cos(a) - cos(a) - 0,7 = 0.
-0,7 = 0.
Это противоречие, так как -0,7 не равно 0.
Таким образом, задача не имеет решений.
Вывод: sin(a+a) не имеет определенного численного значения, так как исходное уравнение противоречиво.