Буду очень благодарен! Решить дифференциальное уравнение:
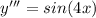
Другие вопросы по теме Математика
Популярные вопросы
- Довжина прямокутника на 5м більша за ширину, а площа становить...
1 - Расставить коэффициенты методом электронного k20+hcl=kcl+h20...
2 - Используй краткую форму - what is your name? she is altynay....
2 - Как вы считаете почему библия одна из самых читаемых книг в...
1 - Формы рельефа в австралийской платформе...
1 - 15 1 метеостанция измеряет давление и записывает минимальным...
3 - Решить кроссворд на тему конёк горбунок по горизонтали 1. начальник...
2 - Нужно написать сочиненее о земледельце по...
3 - Оба выделенных слова пишутся слитно в предложении: варианты...
2 - Небольшое эссе на тему қолғабыс көрсету...
2
Пошаговое объяснение: Три раза интегрируешь и вот все решение