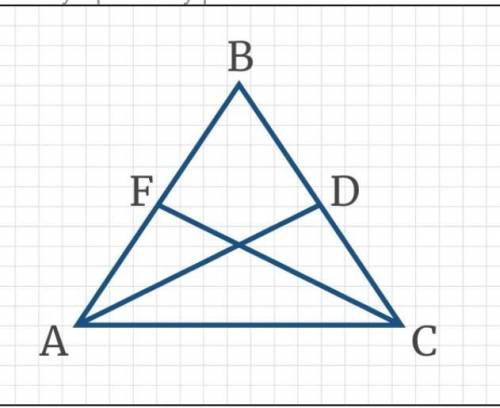
ABC-равнобедренный AD и CF-биссектрисы углов CAB и ACB соответственно. по какому признаку треугольника ADC равен треугольнику

Для решения данной задачи необходимо использование свойств равнобедренных треугольников и биссектрис.

1. В равнобедренном треугольнике основания равны. Таким образом, мы можем сказать, что сторона AB равна стороне AC.

2. Также, в равнобедренном треугольнике углы при основании равны. Следовательно, углы CAB и ACB равны между собой.

3. По свойству биссектрисы, она делит угол на два равных по величине угла. Таким образом, углы DAB и DAC равны между собой.

4. Так как углы CAB, ACB и DAB равны между собой, то углы CAB и DAC также равны друг другу.

5. Теперь рассмотрим треугольник ADC. У него имеются два равных угла - углы DAC и DCA (по признаку равнобедренной конструкции). И углы ACD и CDA (по свойству биссектрисы).

Таким образом, у нас получается два равных треугольника - ABC и ADC. Равенство треугольников обозначается так: ∆ABC ≡ ∆ADC.

В итоге, можно сказать, что треугольник ADC равен треугольнику ABC по двум признакам равнобедренности: равенству сторон AB и AC, а также равенству углов CAB и ACB.