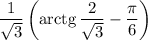4. Найдите интеграл: 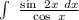 5. Вычислите
5. Вычислите 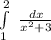 очень заранее огромное
очень заранее огромное
Другие вопросы по теме Математика
Популярные вопросы
- Сочинение на тему Бабушка с малиной...
3 - найдите в тексте описание внешности маленькой разбойници обратите внимание...
3 - задание 3 прочитайте письмо академика Дмитрия лихачева обращенное к юношества...
3 - в настоящее время широко распространяется новые технологии гаджеты социальной...
3 - с физикой На какой глубине, на батискаф в воде, давит давление 10МПа.Плотность...
3 - Тіло розміри якого 10 м,летить зі швидкістю υ=0,6с. Які розмір має тіло...
2 - , решите два логорифма !1) a^2log(a)N 2) 4^-log(4)20...
2 - У партії з 16 яєць є 6 несвіжих. Із партії беруть навмання одне за одним...
2 - 1.Как Саманиды освободились от зависимости халифата? 2.С какого времени...
2 - Сума двох чисел дорівнює 21, а їх добуток 90, Знайдіть ці числа....
3
ответ: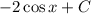
ответ: