2звдние рисунок 1 внизу только с решением

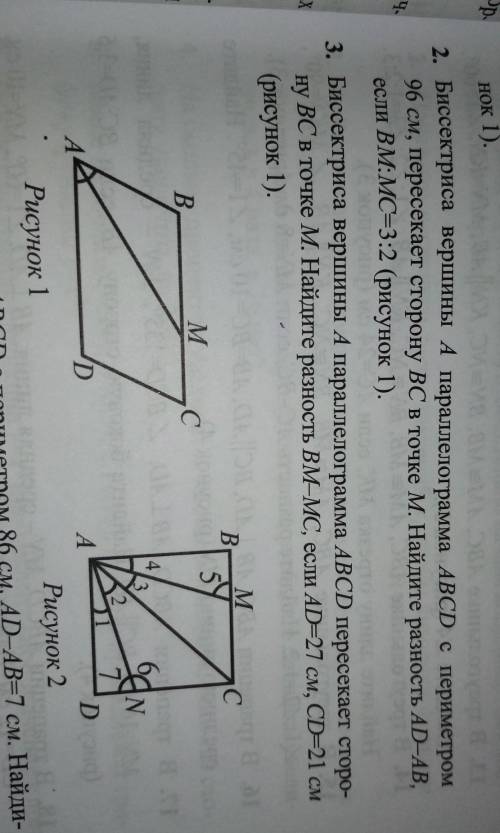
угол ВМА= углу ВАМ как внутренние односторонние при ВС||АД и секущей АМ, значит треугольник АВМ равнобедренный и АВ=ВМ

АВ=ВМ=3х, МС=2х

подставим в периметр:

96= 2(3х+3х+2х)

96=2×8х

16х=96

х=6

АД=3×6+2×6= 18+12=30

АВ=3×6=18

30-18=12

ответ:12

Есть свойство у биссектрисы параллелограмма, где говорится биссектриса угла параллелограмма отсекает от него равнобедренный треугольник, то есть BM=AB.

BM:MC=3:2. Обозначим, как 3x и 2x.

Значит и AB=3x. BC=3x+2x=5x. У параллелограмма параллельные стороны равны, поэтому AB=CD и BC=AD.

Периметр 96.

AB=3x=3×6=18

AD=5x=5×6=30

Нам надо найти AD-AB=30-18=12.

ответ 12