20 вершинами треугольника являются точки а=(-2; 1) в=(-1; 5) с=(-6; 2) докажите что он равнобедренный

AB=√((-2+1)^2+(1-5)^2)=√(1+16)=√17

BC=√((-1+6)^2+(5-2)^2)=√(25+9)=√34

AC=√((-2+6)^2+(1-2)^2)=√(16+1)=√17

АВ=АС,значит,треугольник равнобедренный

Треугольник равнобедренный, если длины двух его сторон равны.

Имеем координаты точек, следовательно, можем найти координаты и длины векторов AB, BC, CA.

Чтобы найти координаты вектора, необходимо от координат конца отнять координаты начала.

Получаем, AB=(-1 - (-2); 5-1) = (1;4), BC=(-6 - (-1); 2-5) = (-5; -3),

CA=(-2 - (-6); 1-2) = (4; -1).

Длина вектора находится по формуле: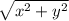 и обозначается, например, |AB|.

Имеем:

|AB| =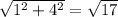

|BC| =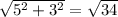

|CA| =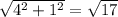

Так как |CA| = |AB|, то треугольник равнобедренный.