123. Решите уравнение:
1)5,6/3х+12=0,4/3
3)3х+1,6/2,4=5/1,2
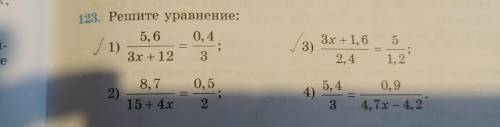
Другие вопросы по теме Математика
Популярные вопросы
- Обчислити масу газу, що утворюється при взаємодії натрій карбону із...
3 - Для решения использовать язык программирования Python...
3 - визнач масштаб карти, якщо одному сантиметру на карті відповідає 30...
1 - обставину виражену порівняльним зворотом ужито в реченні А)Краще кривду...
1 - Упростите выражение 1/4∙ (4a − 12) −1/5∙ (5b + 10) и найдите его значение...
2 - На листе А4 построить два треугольника (остроугольный и тупоугольный)....
1 - Что использовалось для изменения генов растений до генетической модификации?...
3 - 2. Найдите координаты точки пересечения функции у=- 5х +2 с осьюабцисс....
2 - Где находилось родовое кладбище железного периода а)в течении озёр...
2 - Клетки каких живых организмов поражают фаги?...
1
Вариант 1:
основное свойство пропорции (6 класс математика)
если a : b = c : d, то a x d = c x b
для нашего случая получим:
5,6 х 3 = 0,4 х (3х + 12)
16,8 = 1,2х + 4,8
1,2х = 16,8 - 4,8
1,2х = 12
х = 12 : 1,2
х = 10
Вариант 2:
5,6 = 0,4 х 14
3х + 12 = 3 х (х + 4)
< var > \frac{0,4}{3} = \frac{0,4 \cdot 14}{3 \cdot (x+4)} < /var ><var>
3
0,4
=
3⋅(x+4)
0,4⋅14
</var>
это возможно только тогда, когда
< var > \frac{14}{(x+4)} = 1 < /var ><var>
(x+4)
14
=1</var>
получается, что числитель и знаменатель равны
14 = х + 4
х = 14 - 4
х = 10