1 задача (прогрессия)
Тело за первую секунду путь длиной 21,87 мм. За каждую следующую секунду тело проходит путь, который в 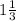раза больше, чем за предыдущую. Сколько потребуется секунд, чтобы тело путь длиной 589,75 мм?
2 задача
Два автомобиля, расстояние между которыми в данный момент равно 795 м. движутся навстречу друг к другу. Скорость 1 автомобиля в этот момент равна 16 м/с, а второго - 19 м/с, после чего, скорости стали увеличиваться. Скорость 1 автомобиля стала увеличиваться на 0,2 м/с, а второго на 0,3 м/с. Через сколько секунд машины встретятся?

Для решения первой задачи нам необходимо определить, какой будет прогрессия пути, который пройдет тело за каждую следующую секунду. Условие говорит нам, что путь будет в "1 1/3" раза больше, чем предыдущий путь.

Давайте начнем с первой секунды, где путь составляет 21,87 мм. Пусть этот путь будет обозначен как а. Значит, за вторую секунду тело пройдет 1 1/3 * а, за третью секунду - 1 1/3 * (1 1/3 * а), и так далее.

Мы можем представить эту прогрессию в виде: а, 1 1/3 * а, (1 1/3)^2 * а, (1 1/3)^3 * а, ...

Теперь у нас есть данные для составления уравнения прогрессии. Мы знаем, что путь тела за вторую секунду составляет 1 1/3 * а, поэтому можно записать следующее:
1 1/3 * а = 21,87 мм

Для решения этого уравнения сначала перейдем от смешанного числа к обычной дроби:
4/3 * а = 21,87 мм

Затем умножим обе части уравнения на 3/4, чтобы избавиться от знаменателя 4/3:
а = (21,87 мм) * (3/4)
а = 65,61 мм

Теперь, когда у нас есть значение а, мы можем использовать его для решения второй части задачи. Нам нужно найти количество секунд, чтобы тело пройдет путь длиной 589,75 мм.

Мы знаем, что путь за первую секунду составляет 65,61 мм, поэтому можно записать следующее:
65,61 мм + 1 1/3 * 65,61 мм + (1 1/3)^2 * 65,61 мм + (1 1/3)^3 * 65,61 мм + ... = 589,75 мм

Здесь мы можем использовать формулу для суммы бесконечной геометрической прогрессии:
S = a / (1 - r)

Где S - сумма прогрессии (в данном случае 589,75 мм), а - первый член прогрессии (в данном случае 65,61 мм), r - знаменатель прогрессии (в данном случае 1 1/3).

Подставив значения в формулу, получим:
589,75 мм = 65,61 мм / (1 - 1 1/3)

Перейдем от смешанного числа к обычной дроби:
589,75 мм = 65,61 мм / (1/3)

Теперь решим уравнение:
589,75 мм = 65,61 мм * (3/1)
589,75 мм = 196,91 мм

Таким образом, тело пройдет путь длиной 589,75 мм через примерно 196,91 секунду.

Для второй задачи нам нужно найти время, через которое два автомобиля встретятся.

Сначала найдем время, через которое они встретятся, пока скорости остаются постоянными. Мы знаем, что расстояние между автомобилями 795 метров, и один из них движется со скоростью 16 м/с, а другой - 19 м/с.

Давайте используем формулу пути: s = v * t, где s - путь, v - скорость, t - время.

Для первого автомобиля:
16 м/с * t = 795 м

Решим это уравнение:
t = 795 м / 16 м/с
t = 49,69 с

Для второго автомобиля:
19 м/с * t = 795 м

Решим это уравнение:
t = 795 м / 19 м/с
t = 41,84 с

Теперь нам нужно учесть, что скорости начинают увеличиваться. Первый автомобиль увеличивается на 0,2 м/с, а второй - на 0,3 м/с.

Для первого автомобиля:
16 м/с + 0,2 м/с * t = v1

Для второго автомобиля:
19 м/с + 0,3 м/с * t = v2

Теперь нам нужно найти время, через которое оба автомобиля встретятся. Пусть это время будет обозначено как t2.

Мы можем сказать, что путь первого автомобиля, пройденный за время t2, равен пути второго автомобиля, пройденному за время t2:
v1 * t2 = v2 * t2

Подставим значения:
(16 м/с + 0,2 м/с * t2) * t2 = (19 м/с + 0,3 м/с * t2) * t2

Раскроем скобки:
16 м/с * t2 + 0,2 м/с * t2^2 = 19 м/с * t2 + 0,3 м/с * t2^2

Перенесем все члены уравнения на одну сторону:
16 м/с * t2 - 19 м/с * t2 + 0,3 м/с * t2^2 - 0,2 м/с * t2^2 = 0

Сократим подобные члены:
-3 м/с * t2 + 0,1 м/с * t2^2 = 0

Теперь решим это квадратное уравнение:
0,1 м/с * t2^2 - 3 м/с * t2 = 0

Разделим на t2:
0,1 м/с * t2 - 3 м/с = 0

Теперь разрешим уравнение:
0,1 м/с * t2 = 3 м/с

Разделим на 0,1 м/с:
t2 = 3 м/с / 0,1 м/с
t2 = 30 с

Таким образом, два автомобиля встретятся через примерно 30 секунд после того, как скорости начали увеличиваться.