1)Выяснить взаимное расположение множеств D, Е, F, если А, В, X — произвольные подмножества универсального множества U(Скриншот 1) 2)Существуют ли множества N, Е, Р такие, что выполняется набор условий В?
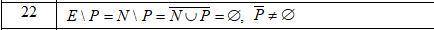
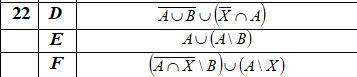
Ответы
Для начала, давайте разберемся с терминологией и определениями, чтобы все было понятно. Множество - это совокупность элементов, которые обладают общим свойством. Универсальное множество - это множество, которое содержит все возможные элементы для данной задачи.
Теперь перейдем к решению первой части вопроса:
1) Выяснить взаимное расположение множеств D, E, F, если A, B, X - произвольные подмножества универсального множества U.
На рисунке дано много информации. Давайте разберемся по порядку.
Множество D: на рисунке оно обозначено зеленым цветом и содержит элементы 1, 2, 3, 4, 5, 6. Эти элементы принадлежат множеству D.
Множество E: на рисунке оно обозначено красным цветом и содержит элементы 3, 4, 5, 6, 7, 8. Эти элементы принадлежат множеству E.
Множество F: на рисунке оно обозначено синим цветом и содержит элементы 1, 2, 3, 7, 8, 9. Эти элементы принадлежат множеству F.
Теперь выясним, какие элементы принадлежат одновременно множествам D, E, F. Для этого мы должны найти пересечение множеств D, E и F.
Пересечение множеств D и E: 3, 4, 5, 6. Они принадлежат как множеству D, так и множеству E.
Пересечение множеств D и F: 1, 2, 3. Они принадлежат как множеству D, так и множеству F.
Пересечение множеств E и F: 3, 7, 8. Они принадлежат как множеству E, так и множеству F.
Теперь нам нужно определить, что означают символы А, В, Х в задаче. Они обозначают произвольные подмножества универсального множества U.
По рисунку видно, что множество А содержит элементы 2, 4, 5, 8. Множество В содержит элементы 1, 3, 6, 9. Множество Х содержит элементы 1, 2, 9.
Итак, теперь мы можем определить взаимное расположение множеств D, E, F относительно множеств A, B, X.
Множество D содержит все элементы, которые есть в множестве А, так как все элементы множества А присутствуют в множестве D. Таким образом, множество D является подмножеством множества А.
Множество E содержит элементы 3, 4, 5, 6, которые есть в множестве А, и дополнительно содержит элементы 7 и 8, которых нет в множестве А. Таким образом, множество E является подмножеством множества А и имеет дополнительные элементы.
Множество F содержит элементы 1, 2, 3, которые есть в множестве А, и дополнительно содержит элементы 7 и 8, которых нет в множестве А. Также множество F содержит дополнительный элемент 9, которого нет в множестве А. Таким образом, множество F является подмножеством множества А и имеет дополнительные элементы.
Таким образом, можно сказать, что множество D является подмножеством множества А, множество E является подмножеством множества А с дополнительными элементами, и множество F является подмножеством множества А с дополнительными элементами.
Теперь перейдем ко второй части вопроса:
2) Существуют ли множества N, E, P такие, что выполняется набор условий В?
Набор условий В говорит, что множество В является подмножеством множества P и множества E.
Чтобы ответить на этот вопрос, нам нужно проверить, является ли множество В подмножеством множества P и множества E.
Множество В содержит элементы 1, 3, 6, 9. Множество P содержит элементы 1, 2, 3, 7, 8, 9. Множество E содержит элементы 3, 4, 5, 6, 7, 8.
Множество В содержит все элементы множества P и множества E, поэтому мы можем сказать, что существуют множества N, E, P, которые удовлетворяют набору условий В.
Я надеюсь, что это подробное объяснение помогло вам понять взаимное расположение множеств D, E, F и решить поставленные задачи. Если у вас еще есть вопросы, не стесняйтесь задавать. Всегда готов помочь!
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
Популярные вопросы
- Кто может решить?= Упр 19 кстати 3...
1 - Эссе на тему Ана тілім мақтанышым 80-70 соз...
2 - 80. Виконайте дії: 1) 38.17 - 4832:16; 2) 3596 - 3596 : (2314...
2 - Політичні новації доби середньовіччя...
2 - 3) Как вы думаете, почему язык можно сравнить с живым орга-...
1 - как.правильно например 576+3=???(7+3)=???...
3 - [=-], и [-=] ССП 1)[=-] , и [-=] ССП 2)[-=], нo[-=] ССП 3)[+-=],...
3 - Чему равно ребро пирамиды если площадь её поверхности равна...
2 - Литература 5 класс коровина страница 7,8 выписать все терменыфольклора...
3 - Распределите слова на две группы: б)с разделительным мягким...
3