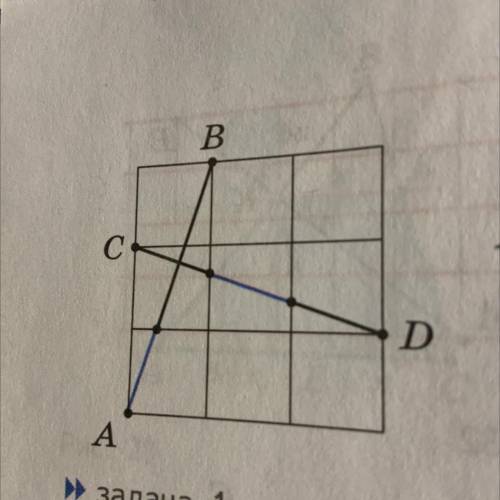
1. В квадрате 3х3 клетки провели отрезки AB и CD так, как это показано
на рисунке. Докажите, что выделенные
части этих отрезков равны. (» рис.)
Другие вопросы по теме Математика
Популярные вопросы
- Выпишите глаголы с зависимыми словами...
3 - Дробь 3\5=х\75.7\у=28\36.6\11=54\х...
2 - Произведение растворимости аg2cr2o7 равно 2х10^-7. выпадает ли осадок...
3 - 7. вычисли значения выражений. (4 + 5) •5 4•6+ (2 + 6) 4 + 5•5 4•(6 +...
2 - Расставьте в порядке возрастания. численность населения стран мира...
3 - Составьте диалог (короткий) можно и много но как вам удобно 25 ...
2 - Как найти свой стиль рисования? дайте советы ...
2 - С) circle the correct word or phrase. 1 it s a great computer programme...
2 - Какай вулкан в америки означает куряшая гора...
1 - 20 ! решите хадачу по при взаємодії 5,4 г алюмінію з сіркою утворились...
3
Для начала, обратим внимание на то, что отрезки AB и CD пересекаются в точке O.
Для доказательства равенства выделенных частей отрезков, воспользуемся сходством треугольников.
Рассмотрим треугольник AOD. Мы можем заметить, что у него есть две пары равных сторон, так как треугольник находится внутри квадрата - сторона AD равна стороне OD, а сторона AO равна стороне DO (как диагональ квадрата).
Теперь обратимся к треугольнику CBO. Здесь также имеется две пары равных сторон – сторона BC равна стороне CO, а сторона BO равна стороне CO.
Теперь мы знаем, что треугольник AOD подобен треугольнику CBO, ведь у них две пары равных сторон. Из свойств подобных треугольников следует, что отношение любой стороны треугольника AOD к соответствующей стороне треугольника CBO будет равно отношению любой другой стороны треугольника AOD к соответствующей стороне треугольника CBO.
Тогда, применим это отношение к сторонам AO и BO:
AO/CO = AD/BC.
Также, мы знаем, что сторона AD равна стороне BC (как стороны квадрата), и, следовательно, можем записать следующее:
AO/CO = AD/AD = 1.
Таким образом, мы получили, что AO/CO = 1.
Из этого следует, что AO равно CO, ведь величина AO и CO определяется длиной соответствующих отрезков.
Это означает, что отрезки AO и CO равны между собой. И также отрезки BO и CO равны между собой.
Таким образом, мы доказали, что выделенные части отрезков AB и CD равны.
Надеюсь, данный ответ был понятен и информативен. Если у вас возникнут дополнительные вопросы, не стесняйтесь задавать их.