1-tg70°tg65°/tg70°+tg65° с этим тригонометрическим выражением подробно объяснить, ибо ответ нашла, а разобрать почему именно так не могу
yanssen1976
1
27.09.2019 07:01
0
Другие вопросы по теме Математика
myafyanya
26.08.2020 19:43
t4rka
27.08.2020 19:01
2303901
26.08.2020 19:29
asdx1984
27.08.2020 07:22
МудрыйКролик
27.08.2020 18:56
Nastya21724
27.08.2020 18:51
Jenyastai
27.08.2020 18:48
vika12325
27.08.2020 18:48
Sherlokzn
27.08.2020 18:47
aaaaaa29
27.08.2020 18:39
Популярные вопросы
- Времена года в музыке Вставь пропущенные слова.Нурали Бейсекожа...
3 - Ханы Белой Орды чеканили свои монеты в городе: а)...
1 - решить контрольную по геометрии...
1 - 7-тапсырма. Мотіннен сабақты және салт етістіктерді тауып, дәптеріне...
1 - Разложите многочлен на множители; 7) 8×1/8а³ ;...
3 - Практическая работа 3 Опыт Наблюдения Уравнение реакции Взаимодействие...
3 - 1. We planted the flowers 2 days ago 2. The wind blew all the leaves...
3 - Бала құқығын қорғау басты міндетіміз эссе(өз ойыңнан нинада копировать...
3 - Волинського князівства?1) Холм; 2) Червен,3) Овруч, 4) Теребовта...
2 - 3.Белая Орда была населена племенами: а) арабоязычными в)...
1
ответ: -1.
Объяснение: используя равенство, что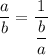
, можем получить в знаменателе формулу тангенса суммы 
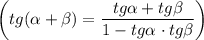. Сложив углы 70° и 65°, получим tg135°, а тангенс такого угла имеет значение -1. И, в таком случае получается ответ -1.
Решение внизу на фото