1. Известно, что (x2 – 6x + 9) + (5y – 3)2 + (4z + +5)4 = 0 Найти 2x +10y – 4z. 1) 16 2) 29 3) 25 4) 17
2. Два пешехода вышли одновременно навстречу друг другу – первый из А. второй из В и встретились через три часа. За сколько времени второй расстояние АВ, если он пришел в В на 2,5 часа позже, чем второй пришел в А. 1) 7 2) 8 3) 5 4) 10

Ответы

nekit1307 02.01.2022 22:11

Задание 1

Вы не поставили знаки возведения в степень (не забывайте их, иначе выражение совсем непонятно- приходится гадать, что за действие там было- умножение или возведение в степень).

Вот это выражение со знаками возведения в степень:

(x^2 - 6x + 9) + (5y - 3)^2 + (4z + 5)^4 = 0

А записав это же в поле уравнение (кнопка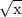 $$\sqrt{\rm x}$ ), получим как на бумаге:

$(x^2 - 6x + 9) + (5y - 3)^2 + (4z + 5)^4 = 0

Решаем:

$(x - 3)^2 + (5y - 3)^2 + (4z + 5)^4 = 0

Отсюда получаем, что все три слагаемых должны быть равны нулю:

$$(x - 3)^2 = 0 \ \ \ \to \ \ \ x - 3 = 0 \ \ \ \to \ \ \ x = 3$

$$(5y - 3)^2 = 0 \ \ \ \to \ \ \ 5y - 3 = 0 \ \ \ \to \ \ \ y = \frac{3}{5}$

$$(4z + 5)^4 = 0 \ \ \ \to \ \ \ 4z + 5 = 0 \ \ \ \to \ \ \ z = -\frac{5}{4}$

Считаем заданное выражение:

$$2x+10y-4z=2\cdot3 + 10\cdot \frac{3}{5} - 4\cdot\!\left(-\frac{5}{4}\right) = 6 + 6 + 5 = 17$

ответ: вариант 4

Задание 2

В тексте задачи опечатка- сравнивается время второго пешехода со вторым же. Если предположить, что правильный текст такой: "За сколько времени первый расстояние АВ", то имеем вот что:

Обозначим величины:

S - расстояние от A до B

t1 - время в пути первого пешехода

t2 - время в пути второго пешехода

v1 - скорость первого пешехода

v2 - скорость второго пешехода

Считаем что они двигались равномерно (не меняя скорости).

Первый и второй до точки встречи шли 3 часа. За это время они суммарно полное расстояние S. Запишем это, вычисляя путь каждого через его скорость и время (3 ч):

$$\rm S=3v_1+3v_2$

Запишем скорости пешеходов через путь и время каждого и подставим в уравнение выше.

$$\rm v_1=\frac{S}{t_1}$

$$\rm v_2=\frac{S}{t_2}$

$$\rm S=3\frac{S}{t_1}+3\frac{S}{t_2}$

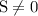Т.к. $$\rm S\ne0$ , то можем поделить обе части уравнения на $$\rm S$ :

$$\rm 1=\frac{3}{t_1}+\frac{3}{t_2}$

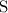Выразим время t2 через t1 (они связаны по условиям задачи), и подставим это выражение вместо t2 в уравнение:

$$\rm t_2=t_1-2{,}5$

$$\rm 1=\frac{3}{t_1}+\frac{3}{t_1-2,\hspace{-0.5mm}5}$

Умножим обе части уравнения на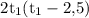 $$\rm 2t_1(t_1-2{,}5)$ :

(при этом нужно указать, что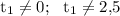 $$\rm t_1\ne0;\ \ t_1\ne2{,}5$ )

$$\rm 2t_1(t_1-2{,}5)=6(t_1-2{,}5)+6t_1$

$$\rm 2t_1^2-5t_1=6t_1-15+6t_1$

$$\rm 2t_1^2-17t_1+15=0$

$$t_{1.1}=\frac{17+\sqrt{(-17)^2-4\cdot2\cdot15}}{2\cdot2}=\frac{17+13}{4}=7{,}5$ (ч)

$$t_{1.2}=\frac{17-\sqrt{(-17)^2-4\cdot2\cdot15}}{2\cdot2}=\frac{17-13}{4}=1$ (ч)

Значение 1 ч не подходит по условиям задачи (оно меньше 3 ч).

А значение 7,5 ч - подходит по условиям задачи, не попадает на указанные ограничения (не равно 0 или 2,5), но отсутствует среди вариантов ответа (если только вы первый вариант не записали с очередной ошибкой- 7 вместо 7,5).

То есть, в таком виде задачи, ответ будет- нет верных вариантов.

Решение будет подходить под эти варианты, только если предположить, что в тексте задачи вообще всё перепутано, и правильный текст на самом деле звучит как то так:

"Два пешехода вышли одновременно навстречу друг другу – первый из пункта А, второй из пункта В. Они встретились через три часа. За сколько времени первый расстояние АВ, если он пришёл в пункт В на 2,5 часа раньше, чем второй пришёл в пункт А."

В этом случае получим такое решение:

$$\rm S=3v_1+3v_2$

$$\rm v_1=\frac{S}{t_1}$

$$\rm v_2=\frac{S}{t_2}$

$$\rm S=3\frac{S}{t_1}+3\frac{S}{t_2}$

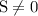Т.к. $$\rm S\ne0$ , то можем поделить обе части уравнения на $$\rm S$ :

$$\rm 1=\frac{3}{t_1}+\frac{3}{t_2}$

$$\rm t_2=t_1+2{,}5$

$$\rm 1=\frac{3}{t_1}+\frac{3}{t_1+2,\hspace{-0.5mm}5}$

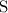Умножим обе части уравнения на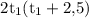 $$\rm 2t_1(t_1+2{,}5)$ :

(при этом нужно указать, что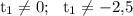 $$\rm t_1\ne0;\ \ t_1\ne-2{,}5$ )

$$\rm 2t_1(t_1+2{,}5)=6(t_1+2{,}5)+6t_1$

$$\rm 2t_1^2+5t_1=6t_1+15+6t_1$

$$\rm 2t_1^2-7t_1-15=0$

$$t_{1.1}=\frac{7+\sqrt{(-7)^2-4\cdot2\cdot(-15)}}{2\cdot2}=\frac{7+13}{4}=5$ (ч)

$$t_{1.2}=\frac{7-\sqrt{(-7)^2-4\cdot2\cdot(-15)}}{2\cdot2}=\frac{7-13}{4}=-1,\hspace{-0.3mm}5$ (ч)

Значение -1,5 ч не подходит по условиям задачи (здесь отрицательное время не имеет смысла).

Значение 5 ч -подходит по условиям задачи, не попадает на указанные ограничения (не равно 0 или -2,5) и присутствует среди вариантов ответа.

ответ: вариант 3

ВЫВОД: сверьте текст задания с исходным- если при наборе действительно были допущены указанные мной ошибки, то вариант решения я привёл выше (и, в следующий раз проверяйте текст перед отправкой задания).

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Математика