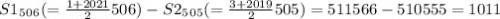(1 + 5 + 9 + 13 + ⋯ + 2017 + 2021) −
(3 + 7 + 11 + ⋯ + 2015 + 2019)
Другие вопросы по теме Математика
Популярные вопросы
- Массу 28,8 магния нагревают с 24 г. оксида кремния. Полученную смесь обрабатывают...
2 - О чём думает Вера Николаевна, узнав о гибели Г.С.Желткова? Чувствует...
2 - Склади формули продуктів реакцій за валентністю елементів та перетвори...
1 - Проанализируйте высказывания Л.Н. Толстого и выполните задания. «Наука...
3 - 24. От прямоугольной пластины отрезали треугольную часть. В результате...
3 - Кратко про многообразие насекомых,не копировать с интернета...
2 - Дамы и господа, соизвольте с задачей, велика необходимость!...
2 - Диференциальное исчисление...
1 - Пошаговое описание П.З Африки -жестколиственные влажные леса 1.название2.Расположение3.Рельеф4.Климат5.Воды6.Почва7.Растения...
2 - ми Випишіть усі числа які діляться окремо на 2,на 3,на 5,на 9,на 10, на...
3
Это выражение можно представить в виде двух арифметических прогрессий (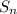 =
=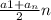 ) нужно посчитать число n 1) d=4 4n-4=2021-1; 4n=2024 n=506; 2)d=4: 4n-4=2019-3; 4n=2020; n=505.
) нужно посчитать число n 1) d=4 4n-4=2021-1; 4n=2024 n=506; 2)d=4: 4n-4=2019-3; 4n=2020; n=505.
Считаем: