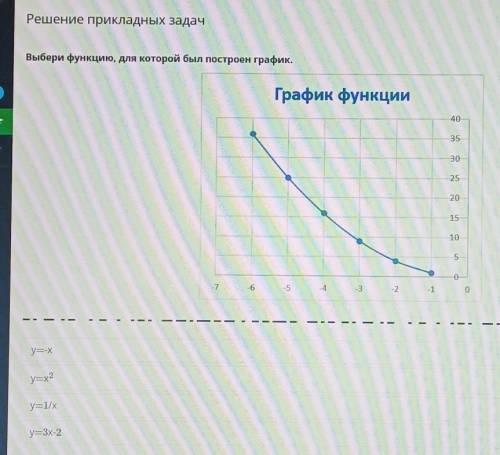
Выбери выбери функцию, для которой был построен график.
Другие вопросы по теме Информатика
Популярные вопросы
- Напишите создания: 2-х-этажного автобуса (в лондоне) или флаг великобритании....
1 - Розв язання за три рейси автомобиль перевиз 12 контейнерив з меблямы. за скильки...
3 - Как определить плотность зная силу архимеда и объем?...
3 - Определи те площадь прямоугольного треугольника со сторонами 4 и 6 см заранее...
1 - Сегодня прекрасная погода .как подчеркнуть главные члены предложения...
3 - Можете написать рассказ о одуваванчике...
2 - А) 4 целых 1\9 x 3 б) (1 целая 1\2+ 2\3) x 6...
1 - Страшила несет 16 булочек а элли 9 на сколько у страшилы больше булочек чем...
2 - Какие бывают сказки? волшебные, о животных и...
2 - Дайте краткую характеристику своего края по плану нижний тагил...
2
Чтобы убедиться в этом, мы можем рассмотреть уравнение этой линии. Для этого выберем две точки на графике и найдем уравнение прямой, проходящей через эти две точки.
Давайте возьмем первую точку, которая находится на левом конце прямой. По графику можно определить, что эта точка имеет координаты (0, 2).
Затем возьмем вторую точку, которая находится на правом конце прямой. По графику можно определить, что эта точка имеет координаты (4, 6).
Теперь мы можем использовать эти две точки для нахождения уравнения прямой с помощью метода нахождения уравнения прямой через две точки.
1. Найдем значение наклона прямой (скорость изменения y в зависимости от изменения x):
Наклон (m) = (y2 - y1) / (x2 - x1)
= (6 - 2) / (4 - 0)
= 4 / 4
= 1
2. Используя найденное значение наклона и одну из точек (например, (0, 2)), можем записать уравнение в виде y = mx + b, где m - наклон и b - y-перехват:
2 = 1 * 0 + b
3. Найдем значение y-перехвата (b):
2 = 0 + b
b = 2
Таким образом, уравнение прямой, изображенной на графике, будет выглядеть следующим образом:
y = x + 2
Итак, на основании анализа графика и нахождения уравнения прямой, мы можем заключить, что функция, для которой был построен этот график, является линейной функцией y = x + 2.