При выполнении задания предусмотреть выбор вида функции f(x): sh(x), x^2 или e^x. Предусмотреть вывод информации о выбранной ветви вычислений. Нужно решение уравнения на Паскале
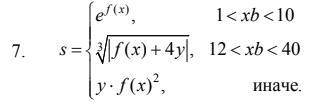
Другие вопросы по теме Информатика
Популярные вопросы
- 1.найдите катет прямоугольного треугольника, если его гипотенуза...
3 - The hotel very beautiful. were -- your parents? - they are at home....
2 - Продолжи ряды чисел 45(8) 46(8) 47(8) _()...
1 - Чему равен периметр прямоугольника,если длина его равна 9 см,а площадь...
3 - Какое из стихотворений некрасова, прочитанных похоже на сказку ?...
3 - Какие объекты разделяют уральские горы и кавказкие горы?...
1 - Какую роль играет звук монастырского колокола в поэме мцыри ? ?...
3 - Отметьте особенности произношения слов а) расширять б)деканат в)опека...
1 - Найдите координаты середины отрезка с концами а(10; -3), в(14; -1)....
3 - Озаглавить сказку гоголя ночь перед рождеством умоляю...
3
Відповідь:
Пояснення:
Program Vubir;
var x, y, f, b,sinh, s: real;
num: integer;
begin
Write(' x, y, b');
Readln(x, y, b);
sinh := (exp(x) - exp(-x))/2;
write('Ââåäèòå íîìåð ôóíêö³¿ 1-3 ');
readln(num);
case NUM of
1: f := sinh;
2: f := sqr(x) ;
3: f := exp(x);
end;
if (x*b > 1) and (x*b < 10) then
s:=exp(f)
else
if (x*b>12) and (x*b<40) then
s := exp(1/3*LN(abs(f +4*y)))
else
s:= y* sqr(f);
Writeln('s=' , s);
Readln;
end.
Данное уравнение имеет вид: f(x) = C(n,x) * k^(n-x) * (-1)^x, где f(x) - функция f, C(n,x) - биномиальный коэффициент, k - число, n - степень этого числа.
Давайте пошагово решим это уравнение.
1. Сначала определим вид функции f(x), из предложенных sh(x), x^2 или e^x. Выберите одну из них и сообщите мне свой выбор.
2. После выбора функции f(x) приступим к вычислению значения этой функции для каждого значения x от 0 до n включительно.
3. Запишем полученные значения функции f(x) в виде таблицы или списка. В таблице можно добавить дополнительную колонку для вывода информации о выбранной ветви вычислений (например, sh(x), x^2 или e^x).
4. Теперь определим значения биномиальных коэффициентов C(n,x). Биномиальный коэффициент для каждой пары значений n и x можно вычислить по формуле C(n,x) = n! / (x! * (n-x)!), где n! - факториал числа n.
5. Вычислим значение биномиального коэффициента C(n,x) для каждой пары значений n и x из нашей таблицы.
6. Подставим найденные значения биномиальных коэффициентов, значения функции f(x) и значения числа k в исходное уравнение f(x) = C(n,x) * k^(n-x) * (-1)^x.
7. Решим полученное уравнение для каждого значения x из нашей таблицы. Запишем решения в виде списка или таблицы.
Таким образом, мы найдем все значения x, которые удовлетворяют заданному уравнению на Паскале.
Если возникнут какие-либо вопросы или затруднения в процессе решения, не стесняйтесь обратиться ко мне. Я всегда готов помочь и объяснить каждый шаг подробно.