Найти минимум функции L, при заданных ограничениях.
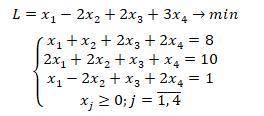
Другие вопросы по теме Информатика
Популярные вопросы
- Орысша қазақша сөздікті пайдаланып мұхтар әуезов туралы айтылған сөздерді...
1 - Значение возникновения и распада империи карла великого...
1 - А)образуйте от следующих прилагательных сравнительную и превосходную...
2 - Сила тяжести дейсивующая на медный шар равна 8.9 ньбтонов. каков его...
2 - Материальная точка, двигавшаяся равноускореннобез начальной скорости...
1 - Внервной ткани есть межклеточное вещество?...
2 - Не выполняя сложения, сравните с числом 1 сумму: б)2/3+3/5. г)1/4+3/7...
2 - По каз. яз. жду ответа6 тапсырма...
3 - Арбир сози болек жазылатын курдели созди тап...
2 - Сторона прямоугольника на 2см больше другой. найти его стороны, если...
2
1. Сначала, давайте запишем заданные ограничения:
Функция g(x, y) = x^2 + 4y^2 - 16 = 0.
Функция h(x, y) = x + 2y - 8 = 0.
2. Теперь, введем множитель Лагранжа λ и запишем функцию Лагранжа:
L(x, y, λ) = f(x, y) + λ * g(x, y) + μ * h(x, y),
где f(x, y) = (x - 2)^2 + (y - 2)^2.
3. Вычислим частные производные функции L по x, y и λ:
∂L/∂x = ∂f/∂x + λ * ∂g/∂x + μ * ∂h/∂x,
∂L/∂y = ∂f/∂y + λ * ∂g/∂y + μ * ∂h/∂y,
∂L/∂λ = g(x, y),
где
∂f/∂x = 2(x - 2), ∂f/∂y = 2(y - 2),
∂g/∂x = 2x, ∂g/∂y = 8y,
∂h/∂x = 1, ∂h/∂y = 2.
4. Поскольку функция L имеет минимум в точке (x, y), то необходимое условие экстремума говорит о том, что все частные производные функции L должны быть равны нулю:
∂L/∂x = 0,
∂L/∂y = 0,
∂L/∂λ = 0.
5. Решим систему из трех уравнений, используя найденные частные производные:
2(x - 2) + λ * 2x + μ = 0,
2(y - 2) + λ * 8y + 2μ = 0,
x^2 + 4y^2 - 16 = 0,
x + 2y - 8 = 0.
6. Решим первые два уравнения системы:
2(x - 2) + λ * 2x + μ = 0, (1)
2(y - 2) + λ * 8y + 2μ = 0. (2)
Умножим (1) на 4 и вычтем (2):
8(x - 2) + 4λx - 4(y - 2) - 8λy = 0,
8x - 16 + 4λx - 4y + 8 - 8λy = 0,
(12λ + 4)x - 4y + (-8λ - 8) = 0. (3)
7. Теперь возьмем второе уравнение системы и подставим в него (3):
2(y - 2) + λ * 8y + 2μ = 0,
2y - 4 + 8λy - 8λy - 8 = 0,
2y - 12 = 0,
y = 6.
8. Вернемся к уравнению (3) и подставим найденное значение y:
(12λ + 4)x - 4y + (-8λ - 8) = 0,
(12λ + 4)x - 4(6) + (-8λ - 8) = 0,
(12λ + 4)x - 24 - 8λ - 8 = 0,
(12λ + 4)x - 8λ - 32 = 0,
12λx + 4x - 8λ - 32 = 0,
(12λ - 8λ)x = 8λ + 32,
4λx = 8λ + 32,
4x = 8 + 32/λ,
x = 2 + 8/λ.
9. Теперь подставим найденные значения x и y в ограничения:
x + 2y - 8 = 0,
2 + 8/λ + 2(6) - 8 = 0,
2 + 8/λ + 12 - 8 = 0,
8/λ + 6 = 0,
8/λ = -6,
8 = -6λ,
λ = -8/6 = -4/3.
10. Наконец, найдем значения x и y:
x = 2 + 8/λ = 2 + 8/(-4/3) = 2 - 6 = -4,
y = 6.
Таким образом, минимум функции L при заданных ограничениях равен (-4, 6).