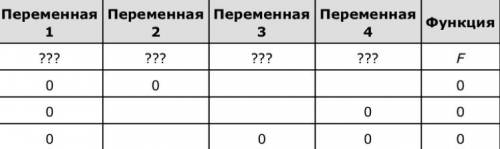
Логическая функция F задаётся выражением (¬x ≡ z) → (y ≡ (w ∨ x)). Дан частично заполненный фрагмент, содержащий неповторяющиеся строки таблицы истинности функции F.
Определите, какому столбцу таблицы истинности соответствует каждая из переменных x, y, z, w. Объясните подробно решение Не надо просто ответ
Другие вопросы по теме Информатика
Популярные вопросы
- Предложение состоящее из четырех слов ,со словом подъём....
3 - Магазин продал 132 телевизора в октябре,в ноябре на 27 телевизоров меньше,чем...
3 - Особенности первичной, вторичной, третичной, четвертичной структуры белка....
3 - 4,27+3,8-5,73-3,3= вычислите более рациональным...
1 - Укажите равенство ,которое является пропорцией 8,4: 2,1=4...
2 - Как правильно прочитать what your name?...
3 - Составить план и аннотацию на произведение х.к. андерсена русалочка...
1 - United kingdom of great britain and northern ireland is made up of england....
2 - Кто наделялся активным и пассивным избирательным правом в древней руси?...
1 - Образуй слова, однокоренные со словом друг...
2
yxwz
Объяснение:
Чтобы значение функции (¬x ≡ z) → (y ≡ (w ∨ x)) было ложным, выражение ¬x ≡ z должно быть истинным, а выражение y ≡ (w ∨ x) – ложным. Чтобы первое выражение было истинным, переменные x и z должны иметь противоположные значения: 0 и 1 или 1 и 0.
Рассмотрим третью строку таблицы. Три переменных равны нулю, F = 0. Значит, оставшаяся переменная (переменная 2 в таблице) равна 1, и это z или x. Тогда y = 0, w = 0, и чтобы выражение y ≡ (w ∨ x) было ложным, необходимо, чтобы x = 1. Значит, второй столбец – x. Другой подходящей комбинации с тремя нулями быть не может, значит, в пустых клетках в первой и второй строках таблицы должны стоять единицы.
Поскольку x и z должны иметь разные значения, а x – это переменная 2, из первой и второй строк таблицы видим, что z – переменная 4.
Рассмотрим вторую строку. В ней x = 1, тогда w ∨ x= 1 независимо от значения w, и чтобы выражение y ≡ (w ∨ x) было ложным, необходимо, чтобы y = 0. Получается, что y – переменная 1, w – переменная 3.