Знайти площу паралелограма АВСД, у якому сторона АВ = 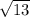см, діагональ ВД = 6 см , а гострий кут між діагоналями дорівнює 60°

12√3 СМ²    или 3√3  см²

Объяснение:  Используем формулу для площади четырехугольника :

S=BD*AC*sin∡BOA/2   (1)

где АС- вторая диагональ параллелограмма. О точка пересечения диагоналей.

Известно, что точка пересечения диагоналей параллелограмма делит диагонали пополам.

Тогда BO=OD=3 cm

Рассмотрим случай, когда ∡ВОА=60°

Тогда из треугольника АВО по теореме косинусов запишем

ВА²=BO²+AO²-2*BO*AO*cos∡BOA

13=9+AO²-3*AO

AO²-3*AO=4

=>AO=4=>AC=8

=> Из (1) запишем

S(ABCD)=8*6*√3/2/2=12√3

Рассмотрим теперь случай , когда острый угол ВОС.  Тогда ∡ВОА=120°

Тогда из ΔАОВ по теореме косинусов  запишем:

ВА²=BO²+AO²+2*BO*AO*cos∡BOA

13=9+AO²+3*AO

AO²+3*AO=4

=>AO=1=>AC=2

=> Из (1) запишем

S(ABCD)=2*6*√3/2/2=3√3 см²