Знайти косинус кута між векторами С (1;0), А(0;1/2)
Другие вопросы по теме Геометрия
Популярные вопросы
- Спервой яблони собрали 21 кг яблок что на 14 кг меньше чем со второи. сколько...
1 - Напишите ваше отношение к французкой диктатуре во время революции в конце...
3 - При скрещивании черных собак породы кокке-спаниель получается потомство четырех...
1 - Вычисли 1+2-3-4+5+6-7-8+9++2010-2011-2012+2013...
1 - Выпишите все крылатые слова и выражения. известно – в самом начале было слово....
3 - 10+2(-3)=4 я никак не могу понять как ответ получился 4 объясните....
3 - Найти область определения функций: 1) у=ln ( 8+x в кубе) 2) y = корень (x-1)(3x+6)...
2 - Закончи следующие предложения 4) john has a mum, 5) john likes...
2 - Что такое краткий анализ 4 действий оперы иван сусанин ? и как его делать...
2 - Составьте предложения где присутствуют двоеточие и тире...
2
ответ: f=90°
Объяснение:
Длина первого вектора d(c) =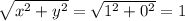
Длина второго вектора d(a) =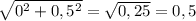
Что бы найти скалярное произведение векторов А и С, нужно переумножить соответствующие координаты векторов и сложить их
(С*А) = 1*0 + 0*0,5 = 0 то есть скалярное произведение равно 0.
Тогда косинус угла f между ними будет cosf= (С*А)/(d(a)*d(c)) = 0
то есть cosf = 0, тогда угол f между векторами f=90°
f=90°