Знаучение sin,cis,tg угла 60°
можно решение

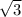sin 60 = /2

cos 60 = 1/2

tg 60 =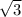

ctg 60 =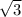 /3

Объяснение:

tg = sin/cos

ctg = cos/sin

ответ: ∠ВАО=30°. (Угол В равен 60 градусам, ∠ВOA
Объяснение
Рассмотрим равносторонний треугольник АВС. Пусть, каждая из его сторон будет равна a. Согласно свойствам равностороннего треугольника, все его углы равны, в том числе угол ∠В=60°.

Значения синуса, косинуса и тангенса мы можем вычислить, если найдем соотношение соответствующих сторон для угла 30 градусов в прямоугольном треугольнике. Так как значение этих тригонометрических функций зависит исключительно от градусной меры угла, то вычисленные нами соотношения и будут значениями синуса 30, косинуса 30 и тангенса 30 градусов.

Сначала совершим дополнительные построения. Из вершины А на сторону BC проведем медиану AO.

Медиана АО в равностороннем треугольнике одновременно является биссектрисой и высотой.

Тогда треугольник АОВ – прямоугольный с углом ∠ВАО=30°. (Угол В равен 60 градусам, ∠ВOA прямой и равен 90 градусам, следовательно, ∠ВАО = 180 - 90 - 60 = 30 градусов)