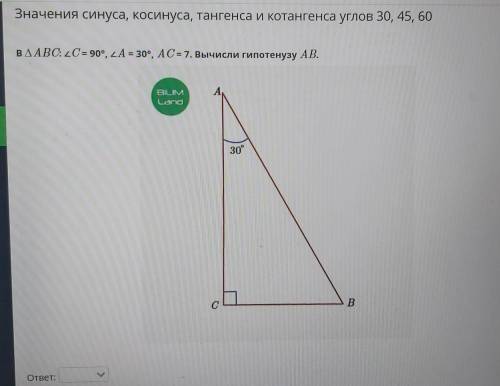
Значения синуса, косинуса, тангенса и котангенса углов 30, 45, 60 в уголАВС: <С = 90°, <А = 30°, АС=7.
Вычисли гипотенузу АВ.
Другие вопросы по теме Геометрия
Популярные вопросы
- Що спільного мають клітини прокаріот і еукаріот ? !...
3 - Вмузее рыболовства кот насчитал 485 больших, средних и маленьких удочек. больших...
1 - Укажите, какой художественный приём использовал а. а. фет в выделенных строках:...
3 - Графики каких линейных функций : 1) у=4х+8 2) у=-5х+11 3) у =4х 4) у=5х 5) у=7х-0,5...
2 - Чего никогда не делал в лагере иван денисович шухов из повести александра исаевича...
2 - Характеристика грицька(дракон) і князя,в оповідані місце для дракона)...
1 - Нада 1. прочитайте. сформулируйте и запишите основную мысль текста. вася и ваня...
2 - Как повлияли на жизнь страны итоги референдума, проведённого 25 апреля 1993 г.?...
2 - Как решить длина стороны прямоугольника 20 сантиметров ширина на 8 сантиметров...
1 - Используя глаголы настоящего и будущего времени, напишите мини - изложение на...
3
cos30°=AC/AB
AB=7÷0.866≈8
Объяснение:
Задача заключается в вычислении гипотенузы АВ, при известных значениях синуса, косинуса, тангенса и котангенса углов 30, 45, 60 в треугольнике АВС.
Шаг 1: Найдем значение синуса, косинуса, тангенса и котангенса угла А. По условию, известно следующее:
- Значение синуса 30 градусов: sin(30) = 1/2
- Значение косинуса 30 градусов: cos(30) = √3/2
- Значение тангенса 30 градусов: tan(30) = 1/(√3)
- Значение котангенса 30 градусов: cot(30) = √3/1
Шаг 2: Рассмотрим треугольник АВС. Мы знаем, что АС = 7 и угол А = 30 градусов. Пусть гипотенуза треугольника АВ равна х, тогда можно записать следующее:
- sin(30) = АС/х
Подставляем известные значения и находим значение переменной х:
1/2 = 7/х
Перекрестно умножаем и решаем уравнение:
2х = 7
х = 7/2
Таким образом, гипотенуза треугольника АВ равна 7/2 или 3.5.
Ответ: Гипотенуза АВ равна 3.5.