Здравствуйте С рисунком и пояснениями

Стороны оснований правильной треугольной усеченной пирамиды ABCA1B1C1 равны 8 см и 5 см, а высота пирамиды - 3 см. Найдите площадь сечения пирамиды плоскостью, проходящей через прямую AB и точку C1.

Ответы

misspolina967 04.05.2021 19:13

S = 24 cм².

Объяснение:

Пирамида правильная, следовательно, основания - правильные треугольники. По формулам радиусы описанных окружностей этих треугольников равны: ОС = R = (√3/3)·а = 8√3/3 см, аналогично,

R1 = 5√3/3 см. Радиус вписанной окружности r = OH = R/2 = 4√3/3 см.

Тогда ОР = ОН +ОР = 4√3/3 + 5√3/3 = 9√3/3 = 3√3 см. (так как ОР = О1С1).

В прямоугольном треугольнике С1НР по Пифагору найдем С1Н - высоту сечения АВС1 (по теореме о трех перпендикулярах).

С1Н = √(НР²+С1Р²) = √(27+9) = 6 см.

Площадь сечения (треугольника АВС1) равна:

S = (1/2)·AB·C1H = (1/2)·8·6 = 24 cм².

Здравствуйте С рисунком и пояснениямиСтороны оснований правильной треугольной усеченной пирамиды ABC

ПОКАЗАТЬ ОТВЕТЫ

foton228 04.05.2021 19:13

Стороны оснований правильной треугольной усеченной пирамиды ABCA1B1C1 равны 8 см и 5 см, а высота пирамиды - 3 см. Найдите площадь сечения пирамиды плоскостью, проходящей через прямую AB и точку C1.

Объяснение:

1) Т.к усеченная пирамида правильная , то АС₁=ВС₁. В сечении ΔАВС₁-равнобедренный треугольник .Найдем площадь по формуле Герона S= √p (p−a) (p−b) (p−c) , где p= 1 ÷2 *(a+b+c) полупериметр.

2) В равносторонних треугольниках ΔАВС, ΔА₁В₁С₁ найдем высоты , по т. Пифагора А₁Н₁=√(5²-2,5²)=√(2,5*7,5)=√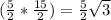 $(\frac{5}{2} *\frac{15}{2} )=\frac{5}{2}\sqrt{3}$ (см),

АН=√(8²-4²)=√(4*12)=4√3 (см).

Высота правильной усеченной пирамиды проходит через центр треугольника , поэтому радиусы вписанных окружностей равны

r₁=О₁Н₁=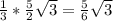 $\frac{1}{3} *\frac{5}{2}\sqrt{3}=\frac{5}{6}\sqrt{3}$ (см),

r=ОН=1/3*4√3=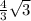 $\frac{4}{3} \sqrt{3}$ (см).

3) В прямоугольной трапеции ОО₁Н₁Н проведем высоту Н₁К. Тогда

КН=ОН-ОК=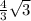 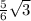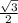$\frac{4}{3} \sqrt{3}$ - $\frac{5}{6}\sqrt{3}$ = $\frac{\sqrt{3} }{2}$ ( см)

ΔКНН₁- прямоугольный , по т. Пифагора НН₁=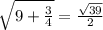 $\sqrt{9+\frac{3}{4} } =\frac{\sqrt{39} }{2}$ ( см).

4) В равнобедренной трапеции СС₁В₁В проведем высоту С₁М .

Тогда МВ=5+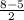 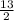$\frac{8-5}{2}$ = $\frac{13}{2}$ ( см)

ΔМС₁В-прямоугольный , по т. Пифагора

С₁В=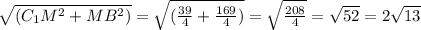 $\sqrt{(C_1M^{2} +MB^{2} )} =\sqrt{(\frac{39}{4}+\frac{169}{4} ) } =\sqrt{\frac{208}{4} } =\sqrt{52} =2\sqrt{13}$ (cм).

С₁А=2√13 см( диагонали в равных равнобедренных трапециях равны)

5) По ф. Герона

$p=\frac{8+2*2\sqrt{13} }{2} =4+2\sqrt{13} \\p-a=4+2\sqrt{13}-8 =2\sqrt{13}-4 \\p-b=4+2\sqrt{13}-2\sqrt{13} =4\\S=\sqrt{(4+2\sqrt{13} )*(2\sqrt{13}-4)*4^{2} } =4*\sqrt{(52-16)} =4\sqrt{36} =24 (cm^{2} )$ .