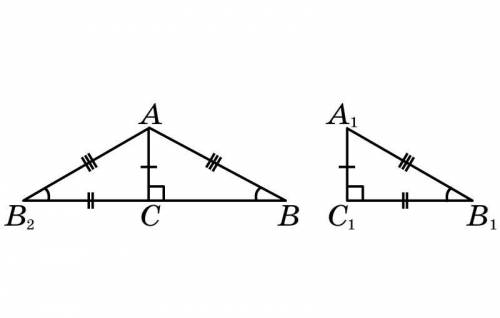
Заполните пропуски в доказательстве признака равенства прямоугольных треугольников по катету и противолежащему углу. Пусть в прямоугольных треугольниках ABC и A1B1C1 с гипотенузами AB и A1B1 равны катеты AC и A1C1 и острые углы ∠B и ∠B1 .

На продолжении катета за точку отложим отрезок , равный . Тогда прямоугольный треугольник ACB2 равен треугольнику по . Значит, ∠B2 = ∠B1 = ∠. Значит, треугольник BAB2 равнобедренный, поэтому AB = AB2 = . Следовательно, треугольник ABC равен треугольнику A1B1C1 по . Признак доказан.

mchermakov17    1   17.12.2020 19:08    32